题目内容
设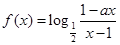 为奇函数,
为奇函数,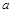 为常数.
为常数.
(1)求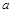 的值;
的值;
(2)证明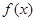 在区间(1,+∞)内单调递增;
在区间(1,+∞)内单调递增;
(3)若对于区间[3,4]上的每一个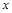 的值,不等式
的值,不等式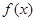 >
>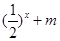 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
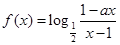 为奇函数,
为奇函数,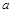 为常数.
为常数.(1)求
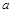 的值;
的值;(2)证明
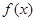 在区间(1,+∞)内单调递增;
在区间(1,+∞)内单调递增;(3)若对于区间[3,4]上的每一个
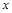 的值,不等式
的值,不等式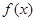 >
>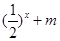 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.(1)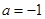 ;(2)证明见解析;(3)
;(2)证明见解析;(3)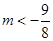 .
.
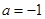 ;(2)证明见解析;(3)
;(2)证明见解析;(3)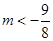 .
.试题分析:(1)利用奇函数的定义找关系求解出字母的值,注意对多解的取舍.
 是奇函数,
是奇函数, ,可解得
,可解得 ,检验
,检验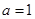 (舍);
(舍);(2)利用单调性的定义证明函数在给定区间上的单调性,关键要在自变量大小的前提下推导出函数值的大小.任取
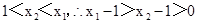
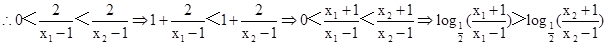
即

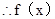 在
在 内单调递增;
内单调递增;(3)将恒成立问题转化为函数的最值问题,用到了分离变量的思想.对
 于上的每一个
于上的每一个 的值,不等式
的值,不等式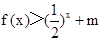 恒成立,即
恒成立,即 恒成立.令
恒成立.令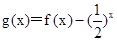 .只需
.只需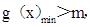
又易知
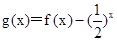 在
在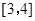 上是增函数,∴
上是增函数,∴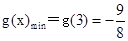
 时原式恒成立.
时原式恒成立.试题解析:
解:(1)
 是奇函数,
是奇函数, .
.
检验
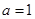 (舍),
(舍),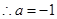 .
.(2)由(1)知
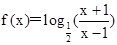
证明:任取
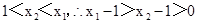

即

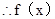 在
在 内单调递增.
内单调递增.(3)对
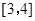 于上的每一个
于上的每一个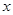 的值,不等式
的值,不等式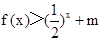 恒成立,即
恒成立,即 恒成立.
恒成立.令
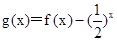 .只需
.只需
又易知
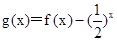 在
在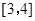 上是增函数,
上是增函数,∴
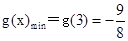
 时原式恒成立.
时原式恒成立.
练习册系列答案
相关题目
 奇偶性相同且在(-∞,0)上单调性也相同的是( ).
奇偶性相同且在(-∞,0)上单调性也相同的是( ).
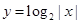
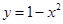
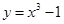
 在区间
在区间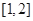 上的最小值是( )
上的最小值是( )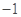

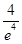
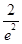
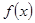 是定义在
是定义在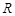 上的偶函数,且在区间
上的偶函数,且在区间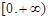 上是单调增函数.如果实数
上是单调增函数.如果实数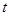 满足
满足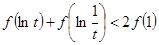 ,则
,则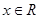 ,奇函数
,奇函数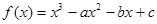 在
在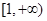 上单调,则字母
上单调,则字母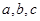 应满足的条件是 .
应满足的条件是 .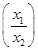 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.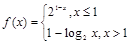 ,则满足
,则满足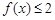 的x的取值范围是 .
的x的取值范围是 .