题目内容
9.对于定义在区间M上的函数f(x),若满足对?x1,x2∈M且x1<x2时,都有f(x1)≤f(x2),则称函数f(x)为区间M上的“非减函数”,若f(x)为区间[0,1]上的“非减函数”,且f(0)=0,f(x)+f(1-x)=1;又当x∈[$\frac{3}{4}$,1]时,f(x)≤2x-1恒成立.有下列命题:①?x∈[0,1],f(x)≥0;②当x1,x2∈[0,1]且x1≠x2时,f(x1)≠f(x2);③f($\frac{1}{7}$)+f($\frac{5}{11}$)+f($\frac{7}{13}$)+f($\frac{6}{7}$)=2;④当x∈[$\frac{3}{4}$,1]时,f(f(x))≤f(x).其中正确命题有( )
| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①③④ |
分析 对于①,由f(0)=0,然后直接利用“非减函数”的定义进行判断;
对于②,由x∈[$\frac{3}{4}$,1]时,f(x)≤2x-1恒成立得到f($\frac{3}{4}$)≤$\frac{1}{2}$,在等式f(x)+f(l-x)=l中,取x=$\frac{1}{2}$得到f($\frac{1}{2}$)=$\frac{1}{2}$,而$\frac{3}{4}$>$\frac{1}{2}$,从而说明f($\frac{3}{4}$)≥$\frac{1}{2}$.利用两边夹的思想得到f($\frac{3}{4}$)=$\frac{1}{2}$.同理得到f($\frac{1}{4}$)=$\frac{1}{2}$.结合新定义即可得到结论;
对于③,结合②的结论及等式f(x)+f(l-x)=l变形即可得到;
对于④,当x∈[$\frac{3}{4}$,1]时,判断f(x)与x的大小关系即可.正确.
解答 解:对于①,因为f(0)=0,所以对?x∈[0,1],根据“非减函数”的定义知f(x)≥0.所以①正确;
对于②,因为当x∈[$\frac{3}{4}$,1]时,f(x)≤2x-1恒成立,
∴f($\frac{3}{4}$)≤$\frac{1}{2}$,
又f(x)+f(l-x)=l,所以f($\frac{1}{2}$)=$\frac{1}{2}$,
由而$\frac{3}{4}$>$\frac{1}{2}$,由“非减函数”的定义可知,所以f($\frac{3}{4}$)≥$\frac{1}{2}$.
所以f($\frac{3}{4}$)=$\frac{1}{2}$.
同理有f($\frac{1}{4}$)=$\frac{1}{2}$.
当x∈[$\frac{1}{4}$,$\frac{3}{4}$]时,由“非减函数”的定义可知,f($\frac{1}{4}$)≤f(x)≤f($\frac{3}{4}$),所以f(x)=$\frac{1}{2}$.所以②不正确;
由②中,当x∈[$\frac{1}{4}$,$\frac{3}{4}$]时,f(x)=$\frac{1}{2}$.可得:
所以③正确;f($\frac{5}{11}$)=f($\frac{7}{13}$)=$\frac{1}{2}$,由f(x)+f(1-x)=1得:f($\frac{1}{7}$)+f($\frac{6}{7}$)=1,
故f($\frac{1}{7}$)+f($\frac{5}{11}$)+f($\frac{7}{13}$)+f($\frac{6}{7}$)=2,故③正确;
对于④,当x∈[$\frac{3}{4}$,1]时,x≥2x-1,因为函数f(x)为区间D上的“非减函数”,
所以f(x)≥f(2x-1),
所以f(f(x))≤f(2x-1)≤f(x).所以④正确.
故正确命题有:①③④.
故选:D
点评 本题考查了命题的真假判断与运用,考查了抽象函数的性质,解答的关键是正确理解新定义,考查了学生的抽象思维能力,是中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 6.635 | B. | 7.897 | C. | 5.024 | D. | 3.841 |
| A. | {x|0≤x<1} | B. | {x|0<x≤1} | C. | {x|0≤x≤1} | D. | {x|x<1} |
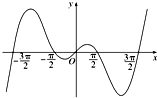
| A. | f(x)=x+sinx | B. | f(x)=x•sinx | C. | f(x)=x•cosx | D. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) |
| A. | 26种 | B. | 32种 | C. | 36种 | D. | 56种 |
