题目内容
4.已知f(x)=sin(2x+$\frac{π}{6}$)+sin2x-$\frac{1}{2}$.(Ⅰ)求函数f(x)的对称中心;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若a=2$\sqrt{3}$,f($\frac{A}{2}$)=$\frac{1}{2}$,cos(π-C)=-$\frac{\sqrt{6}}{3}$,求b的大小.
分析 (Ⅰ)将三角函数进行化简,结合对称中心的方程即可求函数f(x)的对称中心;
(Ⅱ)利用两角和差的正弦公式以及正弦定理进行化简即可.
解答 解:(Ⅰ)f(x)=sin(2x+$\frac{π}{6}$)+sin2x-$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x+$\frac{1-cos2x}{2}-\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x
所以f(x)对称中心是($\frac{kπ}{2}$,0),k∈Z.
(Ⅱ)由f($\frac{A}{2}$)=$\frac{1}{2}$,得f($\frac{A}{2}$)=$\frac{\sqrt{3}}{2}$sinA=$\frac{1}{2}$,
即sinA=$\frac{\sqrt{3}}{3}$,
若cosA=$\frac{\sqrt{6}}{3}$,
而sin(A+C)=$\frac{\sqrt{3}}{3}cosC+\frac{\sqrt{6}}{3}sinC$
又$\sqrt{3}$sin(A+C)=2cosC,
所以cosC=$\sqrt{2}$sinC,
所以cosC=$\frac{\sqrt{6}}{3}$,
所以sinB=sin(A+C)=$\frac{2}{\sqrt{3}}$cosC=$\frac{2\sqrt{2}}{3}$ (10分)
由正弦定理得:b=$\frac{asinB}{sinA}$=4$\sqrt{2}$.(12分)
点评 本题主要考查三角函数的恒等变换以及三角函数的图象和性质,利用两角和差的正弦公式以及正弦定理是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.等差数列{an}中,a3=5,a4+a8=22,则的前20项和为( )
| A. | 400 | B. | 410 | C. | 420 | D. | 430 |
16.下列说法正确的是( )
| A. | “若$x=\frac{π}{3}$,则$sinx=\frac{{\sqrt{3}}}{2}$”的逆命题为真 | |
| B. | a,b,c为实数,若a>b,则ac2>bc2 | |
| C. | 命题p:?x∈R,使得x2+x-1<0,则?p:?x∈R,使得x2+x-1>0 | |
| D. | 若命题?p∧q为真,则p假q真 |
14.已知i为虚数单位,复数z=(1-i)(1+i)的模|z|的值是( )
| A. | 4 | B. | 2 | C. | 4i | D. | 2i |
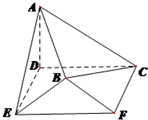 如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.
如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.