题目内容
18.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )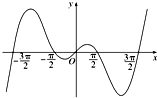
| A. | f(x)=x+sinx | B. | f(x)=x•sinx | C. | f(x)=x•cosx | D. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) |
分析 通过函数的图象的奇偶性、定义域、验证函数的表达式,排除部分选项,利用图象过($\frac{π}{2}$,0),排除选项,得到结果
解答 解:依题意函数是奇函数,排除D,函数图象过原点,排除B,图象过($\frac{π}{2}$,0)显然A不正确,C正确;
故选:C.
点评 本题是基础题,考查函数的图象特征,函数的性质,考查学生的视图能力,常考题型.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
3.在△ABC中,三内角A,B,C的对边分别为a,b,c且a2=b2+c2+bc,a=$\sqrt{3}$,S为△ABC的面积,则S+$\sqrt{3}$cosBcosC的最大值为( )
| A. | 1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$ | D. | 3 |
7. 已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )
 已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )| A. | l∥平面ABCD | |
| B. | l⊥AC | |
| C. | 存在x0∈(0,1),使平面MEF与平面MPQ垂直 | |
| D. | 当x变化时,l是定直线 |
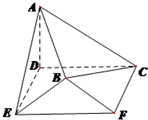 如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.
如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.