题目内容
17.某容量为180的样本的频率分布直方图共有n(n>1)个小矩形,若第一个小矩形的面积等于其余n-1的小矩形的面积之和的$\frac{1}{5}$,则第一个小矩形对应的频数是30.分析 根据频率和为1,求出第1个小矩形对应的频率与频数即可.
解答 解:设第一个小矩形的频率为x,则其余的小矩形频率和为5x,
根据频率和为1,得x+5x=1,
解得x=$\frac{1}{6}$;
所以,第一个小矩形对应的频数是
180×$\frac{1}{6}$=30.
故答案为:30.
点评 本题考查了频率分布直方图的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.函数f(x)=$\sqrt{4{-2}^{x}}$+ln(x-1)的定义域是( )
| A. | (1,2] | B. | [1,2] | C. | (1,+∞) | D. | (-∞,2) |
6.若角α的终边经过点A($\sqrt{3}$,a),且点A在双曲线$\frac{x^2}{3}-{y^2}$=1的渐近线上,则sinα=( )
| A. | ±1 | B. | $±\frac{{\sqrt{2}}}{2}$ | C. | $±\frac{1}{2}$ | D. | $±\frac{{\sqrt{3}}}{2}$ |
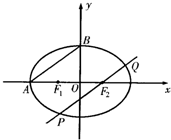 如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.
如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.