题目内容
16.已知抛物线C:y2=2px(p>0)的焦点为F,A(4,1)是抛物线内一点,P在抛物线上,PA+PF的最小值为5.(1)求抛物线方程;
(2)一条直线与抛物线相交于A、B(其中A在第一象限)与x轴、y轴相交于C、D,且|AC|,|CB|,|BD|的比为3:2:1,若这样的直线存在,求出所有符合条件的直线方程;若不存在,说明理由.
分析 (1)易知当AP平行于x轴时PA+PF取最小值为5,利用抛物线的定义计算即得结论;
(2)通过|AC|、|CB|、|BD|的比为3:2:1可知A(2a,-b)、B($\frac{a}{3},\frac{2b}{3}$),代入抛物线方程计算即得结论.
解答 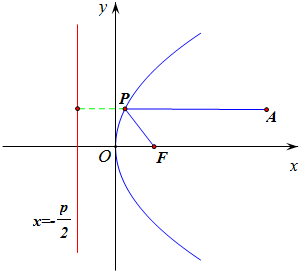 解:(1)如图,当AP平行于x轴时,PA+PF取最小值为5,
解:(1)如图,当AP平行于x轴时,PA+PF取最小值为5,
由抛物线定义可知,点A到抛物线准线x=-$\frac{p}{2}$的距离为5,
又∵A(4,1),
∴4+$\frac{p}{2}$=5,即p=2,
∴抛物线方程为:y2=4x;
(2)∵|AC|、|CB|、|BD|的比为3:2:1,
∴|AC|=|CD|,|CB|=2|BD|,
设C(a,0)、D(b,0),
则A(2a,-b),B($\frac{a}{3},\frac{2b}{3}$),
∵直线与抛物线相交于点A、B,
∴b2=8a,$\frac{{4{b^2}}}{9}=\frac{4a}{3}$,
∴a=0,
∴这样的直线不存在.
点评 本题考查抛物线的简单性质,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.设动点(x,y)满足不等式组$\left\{\begin{array}{l}(x-y+1)(x+y-4)≥0\\ x≥3\end{array}\right.$,则x2+y2的最小值是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $\frac{17}{2}$ | D. | 10 |
1.已知命题p:?α∈R,cos (π-α)=cos α;命题q:?x∈R,x2+1>0.则下面结论正确的是( )
| A. | p∨q是真命题 | B. | p∧q是假命题 | C. | ¬q是真命题 | D. | p 是假命题 |
6.若角α的终边经过点A($\sqrt{3}$,a),且点A在双曲线$\frac{x^2}{3}-{y^2}$=1的渐近线上,则sinα=( )
| A. | ±1 | B. | $±\frac{{\sqrt{2}}}{2}$ | C. | $±\frac{1}{2}$ | D. | $±\frac{{\sqrt{3}}}{2}$ |
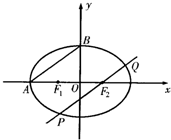 如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.
如图所示,F1、F2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为$\frac{\sqrt{5}}{5}$,△ABO的面积为$\sqrt{5}$.