题目内容
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.

(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)根据椭圆中的![]() ,以及
,以及![]() ,和点到直线的距离公式计算求得
,和点到直线的距离公式计算求得![]() ;(Ⅱ)分斜率不存在和斜率存在两种情况讨论,当斜率存在时,设直线为
;(Ⅱ)分斜率不存在和斜率存在两种情况讨论,当斜率存在时,设直线为![]() 与椭圆方程联立,利用根与系数的关系计算
与椭圆方程联立,利用根与系数的关系计算![]() ,从而求得斜率
,从而求得斜率![]() 和直线方程.
和直线方程.
试题解析:(Ⅰ)由直线![]() ,∴
,∴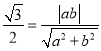 ,即
,即![]() ——①
——①
又由![]() ,得
,得![]() ,即
,即![]() ,又∵
,又∵![]() ,∴
,∴![]() ——②
——②
将②代入①得,即![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
∴所求椭圆方程是![]() ;
;
(Ⅱ)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 方程为
方程为![]() ,
,
则直线![]() 与椭圆的交点为
与椭圆的交点为![]() ,又∵
,又∵![]() ,
,
∴![]() ,即以
,即以![]() 为直径的圆过点
为直径的圆过点![]() ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程为
方程为![]() ,
, ![]() ,
, ![]() ,
,
由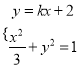 ,得
,得![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]()
∵以![]() 为直径的圆过点
为直径的圆过点![]() ,∴
,∴![]() ,即
,即![]() ,
,
由![]() ,
, ![]() ,
,
得![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() ,即
,即![]() ;
;
综上所述,当以![]() 为直径的圆过定点
为直径的圆过定点![]() 时,直线
时,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案【题目】某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1﹣50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮测试的成绩大于或等于80分视为优秀,小于80分视为不优秀,如表是甲、乙两人分别抽取的样本数据: 甲抽取的样本数据
编号 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 | 47 |
性别 | 男 | 女 | 男 | 男 | 女 | 男 | 女 | 男 | 女 | 女 |
投篮成 绩 | 90 | 60 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 60 |
乙抽取的样本数据
编号 | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 |
性别 | 男 | 男 | 男 | 男 | 男 | 男 | 女 | 女 | 女 | 女 |
投篮成 绩 | 95 | 85 | 85 | 70 | 70 | 80 | 60 | 65 | 70 | 60 |
(Ⅰ)在乙抽取的样本中任取3人,记投篮优秀的学生人数为X,求X的分布列和数学期望.
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
优秀 | 非优秀 | 合计 | |
男 | |||
女 | |||
合计 | 10 |
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)