题目内容
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC. 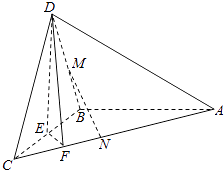
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
【答案】
(1)解:∵△BCD是正三角形,AB⊥平面BCD,AB=BC=a,
∴三棱锥D﹣ABC的体积V= ![]() =
= ![]()
(2)证明:取AC的中点H,∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF
(3)解:连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO= ![]() CM.
CM.
当CN= ![]() CA时,CF=
CA时,CF= ![]() CN,∴MN∥OF.
CN,∴MN∥OF.
∵MN平面DEF,OF平面DEF,
∴MN∥平面DEF.
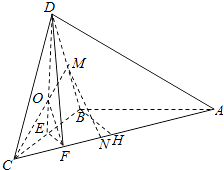
【解析】(1)直接利用体积公式,求三棱锥D﹣ABC的体积;(2)要证AC⊥平面DEF,先证AC⊥DE,再证AC⊥EF,即可.(3)M为BD的中点,连CM,设CM∩DE=O,连OF,只要MN∥OF即可.
【考点精析】解答此题的关键在于理解构成空间几何体的基本元素的相关知识,掌握点、线、面是构成几何体的基本元素,以及对直线与平面平行的判定的理解,了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目