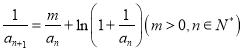题目内容
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(Ⅱ)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
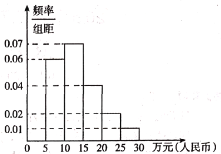
以(Ⅰ)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: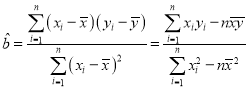 ,
,![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)可以超过
;(Ⅱ)可以超过
【解析】
(1)根据给出的数据计算![]() 和
和![]() ,从而得到回归方程;(2)到2035年底对应的年份代号为23,将
,从而得到回归方程;(2)到2035年底对应的年份代号为23,将![]() 代入,预测出在2035年底人均国民生产总值,计算出平均生产总值,再根据频率分布直方图估计出人均国民生产总值平均数,比较后即可得出结论.
代入,预测出在2035年底人均国民生产总值,计算出平均生产总值,再根据频率分布直方图估计出人均国民生产总值平均数,比较后即可得出结论.
解:(Ⅰ) ![]() ,
,![]() ,
,
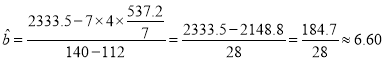 ,
,
![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ;
;
(Ⅱ)到2035年底对应的年份代号为23,
由(Ⅰ)的回归方程![]() 得,2035年我国国内生产总值约为
得,2035年我国国内生产总值约为
![]() 万亿元人民币,
万亿元人民币,
又![]() ,所以到2035年底我国人均国民生产总值约为
,所以到2035年底我国人均国民生产总值约为![]() 万元人民币,
万元人民币,
由直方图,假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值为:
![]() ,
,
又![]() ,所以以(Ⅰ)的结论为依据,可预测我国在2035年底人均国民生产总值可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
,所以以(Ⅰ)的结论为依据,可预测我国在2035年底人均国民生产总值可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.

【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 为解释变量,
为解释变量,![]() 为预报变量,若以
为预报变量,若以![]() 为回归方程,则相关指数
为回归方程,则相关指数![]() ;若以
;若以![]() 为回归方程,则相关指数
为回归方程,则相关指数![]() .
.
(1)判断![]() 与
与![]() 哪一个更适宜作为国内生产总值(GDP)近似值
哪一个更适宜作为国内生产总值(GDP)近似值![]() 关于年份代号
关于年份代号![]() 的回归方程,并说明理由;
的回归方程,并说明理由;
(2)根据(1)的判断结果及表中数据,求出![]() 关于年份代号
关于年份代号![]() 的回归方程(系数精确到
的回归方程(系数精确到![]() );
);
(3)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
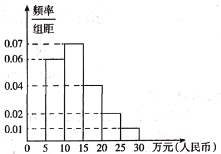
以(2)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: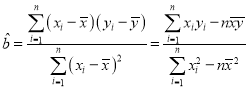 ,
,![]() .
.
【题目】某疾病有甲、乙两种类型,对甲型患者的有效治疗只能通过注射药物Y,而乙型患者可以服药物A进行有效治疗,对该疾病患者可以通过药物A的临床检验确定甲型或乙型.检验的方法是:如果患者利用药物A完成第一个疗程有效,就可以确定是乙型;否则进行第二个疗程,如果完成第二个疗程有效,也可以确定是乙型,否则确定是甲型.为了掌握这种疾病患者中甲型、乙型所占比例,随机抽取100名患者作为样本通过药物A进行临床检验,检验结果是:样本中完成第二个疗程有效的患者是完成第一个疗程有效的患者的60%,且最终确定为甲型患者的有36人.
(1)根据检验结果,将频率视作概率,在利用药物A完成第一个疗程无效的患者中仼选3人,求其中甲型患者恰为2人的概率;
(2)该疾病的患者通过治疗,使血浆中某物质t的浓度降低到![]() 或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:
或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:![]() )的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数
)的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数![]() 和每个疗程后样本血浆中t的平均浓度
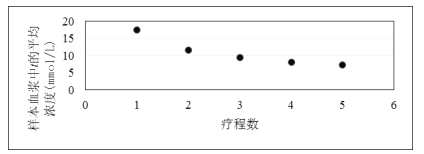
和每个疗程后样本血浆中t的平均浓度![]() 的数据作了初步处理,得到下面的散点图及一些统计量的值.
的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
3 | 11.0 | 0.46 | 262.5 | 30.1 | 55 | 1.458 |
/span>
上表中![]() ,
,![]() .
.
①根据散点图直接判断(不必说明理由),![]() 与
与![]() 哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
②患者在享受基本医疗保险及政府专项补助后,自己需承担的费用z(单位:元)与x,y的关系为![]() .在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
.在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为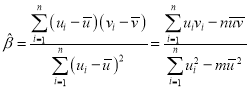 ,
,![]() .
.
【题目】某精密仪器生产厂准备购买![]() ,
,![]() ,
,![]() 三种型号数控车床各一台,已知这三台车床均使用同一种易损件.在购进机器时,可以额外购买这种易损件作为备件,每个0.1万元.在机器使用期间,如果备件不足再购买,则每个0.2万元.现需要决策在购买机器时应同时购买几个易损件,为此搜集并整理了三种型号各120台车床在一年使用期内更换的易损零件数,得到如下统计表:
三种型号数控车床各一台,已知这三台车床均使用同一种易损件.在购进机器时,可以额外购买这种易损件作为备件,每个0.1万元.在机器使用期间,如果备件不足再购买,则每个0.2万元.现需要决策在购买机器时应同时购买几个易损件,为此搜集并整理了三种型号各120台车床在一年使用期内更换的易损零件数,得到如下统计表:
每台车床在一年中更换易损件的件数 | 5 | 6 | 7 | |
频数 |
| 60 | 60 | 0 |
| 30 | 60 | 30 | |
| 0 | 80 | 40 | |
将调查的每种型号车床在一年中更换的易损件的频率视为概率,每台车床在易损件的更换上相互独立.
(Ⅰ)求一年中![]() ,
,![]() ,
,![]() 三种型号车床更换易损件的总数超过18件的概率;
三种型号车床更换易损件的总数超过18件的概率;
(Ⅱ)以一年购买易损件所需总费用的数学期望为决策依据,问精密仪器生产厂在购买车床的同时应购买18件还是19件易损件?