题目内容
【题目】已知数列![]() 满足
满足![]() ,
,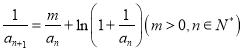 .求证:当
.求证:当![]() 时,
时,
(Ⅰ)![]() ;
;
(Ⅱ)当![]() 时,有
时,有![]() ;
;
(Ⅲ)当![]() 时,有
时,有![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)见解析
【解析】
(Ⅰ)通过数学归纳法,即可证明![]() ;
;
(Ⅱ)先通过构造函数![]() ,利用其单调性
,利用其单调性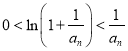 ,对递推公式放缩,得到
,对递推公式放缩,得到![]() ,再利用累乘法即可证明
,再利用累乘法即可证明![]() ;
;
(Ⅲ)通过构造函数![]() ,由导数证明
,由导数证明![]() 在
在![]() 上恒成立,从而得
上恒成立,从而得![]() ,再根据放缩法可得
,再根据放缩法可得![]() ,变形得到
,变形得到![]() ,由累乘法即可证出.
,由累乘法即可证出.
(Ⅰ)用数学归纳法进行证明.
①当![]() 时,
时,![]() 成立;
成立;
②假设当![]() 时,有
时,有![]() 成立,则当
成立,则当![]() 时,有
时,有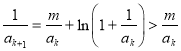 ,又
,又![]() ,故
,故![]() ,综上,可知当
,综上,可知当![]() 时,均有
时,均有![]() .
.
(Ⅱ)设![]() ,则
,则![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() .
.
因为 ,即
,即![]() ,
,
当![]() 时,由累乘法可得,
时,由累乘法可得,![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() ;
;
因为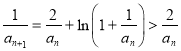 ,即
,即![]() ,
,
当![]() 时,由累乘法可得,
时,由累乘法可得,![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() ,
,
故当![]() 时,有
时,有![]() ;
;
(Ⅲ)由(Ⅱ)可知, 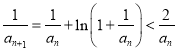 ,即
,即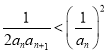 ,且
,且![]() .
.
设![]() ,
,![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以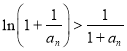 ,
,
因为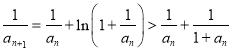 ,
,
即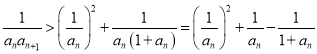 ,且
,且![]() ,
,
所以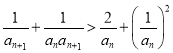 ,即
,即 ,
,
故有![]() ,变形为
,变形为![]() ,
,
当![]() 时,所以
时,所以![]() ,
,
又![]() ,即
,即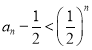 ,所以
,所以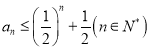 .
.

【题目】在脱贫攻坚中,某市教育局定点帮扶前进村![]() 户贫困户.驻村工作队对这
户贫困户.驻村工作队对这![]() 户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限
户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限![]() 年”与“家庭平均受教育年限
年”与“家庭平均受教育年限![]() 年”,具体调査结果如下表所示:
年”,具体调査结果如下表所示:
平均受教育年限 | 平均受教育年限 | 总计 | |
绝对贫困户 | 10 | 40 | 50 |
相对贫困户 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
(1)为了参加扶贫办公室举办的贫困户“谈心谈话”活动,现通过分层抽样从“家庭平均受教育年限![]() 年”的
年”的![]() 户贫困户中任意抽取
户贫困户中任意抽取![]() 户,再从所抽取的
户,再从所抽取的![]() 户中随机抽取
户中随机抽取![]() 户参加“谈心谈话”活动,求至少有
户参加“谈心谈话”活动,求至少有![]() 户是绝对贫困户的概率;
户是绝对贫困户的概率;
(2)根据上述表格判断:是否有![]() 的把握认为贫困程度与家庭平均受教育程度有关?
的把握认为贫困程度与家庭平均受教育程度有关?
参考公式:![]()
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(Ⅱ)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
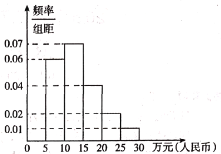
以(Ⅰ)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: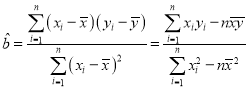 ,
,![]() .
.