题目内容
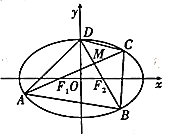
【题目】如图,椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作两条相互垂直的直线
分别作两条相互垂直的直线![]() ,
,![]() ,分别交椭圆
,分别交椭圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 的交点为
的交点为![]() ,三角形
,三角形![]() 面积的最大值为1.
面积的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)当四边形![]() 的面积
的面积![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由已知可得![]() ,根据面积公式及基本不等式可得
,根据面积公式及基本不等式可得![]() ,计算求得
,计算求得![]() ,进而可得
,进而可得![]() 即可得出结果;
即可得出结果;
(2)设直线![]() :
:![]() ,则直线
,则直线![]() :
:![]() ,分别与椭圆方程联立,根据弦长公式及韦达定理化简可得
,分别与椭圆方程联立,根据弦长公式及韦达定理化简可得![]() ,令
,令![]() ,化简可得
,化简可得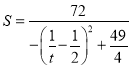 ,根据二次函数性质可知
,根据二次函数性质可知![]() ,进而得出
,进而得出![]() ,通过直线方程联立可求得交点坐标.
,通过直线方程联立可求得交点坐标.
(1)∵![]() ,∴
,∴![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,
当且仅当![]() 时取得最大值
时取得最大值![]() ,∴
,∴![]() ,
,![]() ,
,
∵椭圆![]() 的离心率
的离心率![]() ,∴
,∴![]() ,
,
又由![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() :
:![]() ,由
,由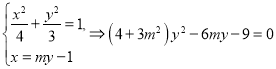 ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
 ,
,
若![]() ,
,![]() ,这时
,这时![]() ,
,![]() ,
,
若![]() ,则直线
,则直线![]() :
:![]() ,
,
由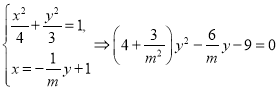 ,
,
同理得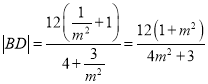 ,
,
∴![]() .
.
设![]() ,则
,则![]() (
(![]() ),
),
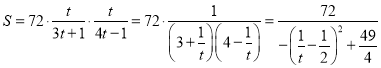 ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,
,
这时![]() ,
,![]() ,
,
当![]() 时,
时,![]() :
:![]() ,
,![]() :
:![]() ,
,
由![]()
当![]() 时,
时,![]() :
:![]() ,
,![]() :
:![]() ,
,
由![]()
故当![]() 最小时,点
最小时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(Ⅱ)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
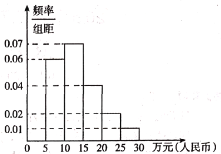
以(Ⅰ)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: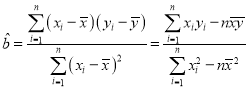 ,
,![]() .
.