题目内容
【题目】已知奇函数f(x)![]() ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
【答案】(1)b=0;(2)在[0,1]上的单调递增,证明见解析;(3)![]()
【解析】
(1)根据函数f(x)![]() 为奇函数,令f(0)=0求解.
为奇函数,令f(0)=0求解.
(2)函数f(x)在[0,1]上的单调递增,再利用函数的单调性定义证明.
(3)根据(2)知,函数f(x)在[0,1]上的单调递增,得到![]() .即g(θ)的最小值为
.即g(θ)的最小值为![]() ,再令t=sinθ,转化为二次函数求解.
,再令t=sinθ,转化为二次函数求解.
(1)因为函数f(x)![]() 为R上的奇函数,
为R上的奇函数,
所以f(0)=0,解得b=0.
(2)函数f(x)在[0,1]上的单调递增.
证明:设![]()
则:f(x2)﹣f(x1)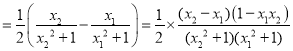 ,
,
因为![]() ,
,
所以x2﹣x1>0,1﹣x1x2>0,
所以![]() ,
,
即f(x2)![]() f(x1),
f(x1),
所以函数f(x)在[0,1]上的单调递增.
(3)由(2)得:函数f(x)在[0,1]上的单调递增,
所以![]() .所以g(θ)的最小值为
.所以g(θ)的最小值为![]() .
.
令t=sinθ,所以y![]() 的最小值为
的最小值为![]() ,
,
令![]()
解得![]()
所以![]() ,
,
即![]() ,
,
所以![]()
又因为θ∈[m,![]() ].m,b∈R,
].m,b∈R,
所以![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目