题目内容
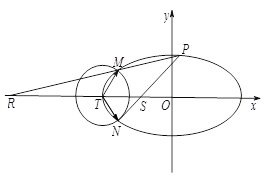
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的左顶点
的左顶点![]() 为圆心作圆
为圆心作圆![]() :
:![]() ,设圆
,设圆![]() 与椭圆
与椭圆![]() 交于点
交于点![]() 与点
与点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,且直线
的任意一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() 为坐标原点,
为坐标原点,
求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,证明见解析.
,证明见解析.
【解析】
试题(1)先通过离心率求出![]() ,再通过
,再通过![]() ,然后写出椭圆方程;(2)先设出
,然后写出椭圆方程;(2)先设出![]() 点的坐标,由于点
点的坐标,由于点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,找到
,找到![]() 向量坐标,根据点乘列出表达式,配方法找到表达式的最小值,得到
向量坐标,根据点乘列出表达式,配方法找到表达式的最小值,得到![]() 点坐标,点
点坐标,点![]() 在圆上,代入得到圆的半径,就可以得到圆的方程;(3)设出点
在圆上,代入得到圆的半径,就可以得到圆的方程;(3)设出点![]() 的坐标,列出直线
的坐标,列出直线![]() 的方程,因为直线与
的方程,因为直线与![]() 轴有交点,所以令
轴有交点,所以令![]() ,得到
,得到![]() ,所以
,所以![]() ,又因为点
,又因为点![]() 在椭圆上,得到方程,代入
在椭圆上,得到方程,代入![]() 中,得到
中,得到![]() ,所以
,所以![]() .
.
试题解析:(1)依题意,得![]() ,
,![]() ,∴
,∴![]() ;
;
故椭圆![]() 的方程为
的方程为![]() . 3分
. 3分
(2)方法一:点![]() 与点
与点![]() 关于
关于![]() 轴对称,设
轴对称,设![]() ,
,![]() , 不妨设
, 不妨设![]() .
.
由于点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() . (*) 4分
. (*) 4分
由已知![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
![]()
![]() . 6分
. 6分
由于![]() ,故当
,故当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.
由(*)式,![]() ,故
,故![]() ,又点
,又点![]() 在圆
在圆![]() 上,代入圆的方程得到
上,代入圆的方程得到![]() .
.
故圆![]() 的方程为:
的方程为:![]() . 8分
. 8分
方法二:点![]() 与点
与点![]() 关于
关于![]() 轴对称,故设
轴对称,故设![]() ,
,
不妨设![]() ,由已知
,由已知![]() ,则
,则
![]()
![]()
![]() . 6分
. 6分
故当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() ,此时
,此时![]() ,
,
又点![]() 在圆
在圆![]() 上,代入圆的方程得到
上,代入圆的方程得到![]() .
.
故圆![]() 的方程为:
的方程为:![]() . 8分
. 8分
(3) 方法一:设![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,
令![]() ,得
,得![]() , 同理:
, 同理:![]() , 10分
, 10分
故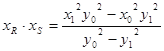 (**) 11分
(**) 11分
又点![]() 与点
与点![]() 在椭圆上,故
在椭圆上,故![]() ,
,![]() , 12分
, 12分
代入(**)式,得: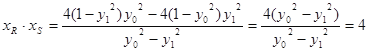 .
.
所以![]() 为定值. 14分
为定值. 14分
方法二:设![]() ,不妨设
,不妨设![]() ,
,![]() ,
,
其中![]() .则直线
.则直线![]() 的方程为:
的方程为:![]() ,
,
令![]() ,得
,得![]() ,
,
同理:![]() , 12分
, 12分
故![]() .
.
所以![]() 为定值. 14分
为定值. 14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】调查某校高三年级男生的身高,随机抽取40名高三男生,实测身高数据(单位:cm)如下:
171 | 163 | 163 | 166 | 166 | 168 | 168 | 160 | 168 | 165 |
171 | 169 | 167 | 169 | 151 | 168 | 170 | 168 | 160 | 174 |
165 | 168 | 174 | 159 | 167 | 156 | 157 | 164 | 169 | 180 |
176 | 157 | 162 | 161 | 158 | 164 | 163 | 163 | 167 | 161 |
(1)作出频率分布表;
(2)画出频率分布直方图.
【题目】已知函数![]() 定义域为
定义域为![]() ,部分对应值如表,
,部分对应值如表,![]() 的导函数
的导函数![]() 的图象如图所示. 下列关于函数
的图象如图所示. 下列关于函数![]() 的结论正确的有( )
的结论正确的有( )
|
|
|
|
|
|
|
|
|
|
|
|

A.函数![]() 的极大值点有
的极大值点有![]() 个
个
B.函数在![]() 上
上![]() 是减函数
是减函数
C.若![]() 时,
时,![]() 的最大值是
的最大值是![]() ,则
,则![]() 的最大值为4
的最大值为4
D.当![]() 时,函数
时,函数![]() 有
有![]() 个零点
个零点