题目内容
18.已知数列{an}是各项均不为0的等差数列,Sn为其前n项和,且满足an2=S2n-1(n∈N*).若不等式$\frac{{λ{{({-1})}^n}}}{{{a_{n+1}}}}≤\frac{{n+8•{{({-1})}^{n+1}}}}{n}$对任意的n∈N*恒成立,则实数λ的取值范围是$[{-\frac{77}{3},-15}]$.分析 由等差数列的性质结合已知递推式可得数列通项公式,把an+1代入不等式$\frac{{λ{{({-1})}^n}}}{{{a_{n+1}}}}≤\frac{{n+8•{{({-1})}^{n+1}}}}{n}$,分n为偶数和奇数分离λ,然后由数列的单调性求得最值得λ的范围,最后取交集得答案.
解答 解:∵数列{an}是各项均不为0的等差数列,且an2=S2n-1,
∴${S_{2n-1}}=(2n-1){a_n}=a_n^2$,则an=2n-1,
当n为偶数时,由不等式$\frac{{λ{{({-1})}^n}}}{{{a_{n+1}}}}≤\frac{{n+8•{{({-1})}^{n+1}}}}{n}$得:
$\frac{λ}{2n+1}≤\frac{n-8}{n}$,即$λ≤\frac{(n-8)(2n+1)}{n}$,
函数$y=\frac{(n-8)(2n+1)}{n}=2n-\frac{8}{n}-15$是增函数,当n=2时取得最小值-15,∴λ≤-15;
当n为奇数时,由不等式$\frac{{λ{{({-1})}^n}}}{{{a_{n+1}}}}≤\frac{{n+8•{{({-1})}^{n+1}}}}{n}$得:
$-λ≤\frac{(n+8)(2n+1)}{n}=2n+\frac{8}{n}+17$,函数$y=2n+\frac{8}{n}+17$,
当n=3时取得最小值为$\frac{77}{3}$,即$-λ≤\frac{77}{3}$,∴$λ≥-\frac{77}{3}$.
综上,λ的取值范围是$[{-\frac{77}{3},-15}]$.
故答案为:$[{-\frac{77}{3},-15}]$.
点评 本题考查数列的递推式,考查等差关系的确定,考查了数列的函数特性,是中档题.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案| A. | -3 | B. | 3 | C. | $\frac{16}{3}$ | D. | ±3 |
| A. | [1,2] | B. | [1,+∞) | C. | $(0,\sqrt{5}]$ | D. | $[1,\sqrt{5}]$ |
| A. | 22014-1 | B. | 22015-1 | C. | 22015+1 | D. | 22016-1 |
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
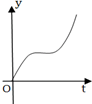
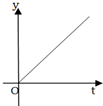
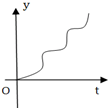
 如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )
如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )