题目内容
已知{an}是正数组成的数列,a1=1,且点(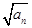 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式;
(2)若数列 满足b1=1,
满足b1=1,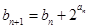 ,求证:
,求证: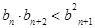 .
.
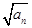 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上.(1)求数列{an}的通项公式;
(2)若数列
 满足b1=1,
满足b1=1,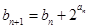 ,求证:
,求证: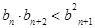 .
.(1) ; (2) 证明过程见试题解析.
; (2) 证明过程见试题解析.
 ; (2) 证明过程见试题解析.
; (2) 证明过程见试题解析.试题分析:(1)将点的坐标代入函数可得an+1-an=1,知
 是以1为公差,1为首项的等差数列,可得通项公式;(2)由所给条件,可得
是以1为公差,1为首项的等差数列,可得通项公式;(2)由所给条件,可得 ,对n分别取值后,用累加法得出
,对n分别取值后,用累加法得出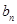 的通项公式
的通项公式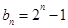 ,则
,则 ,命题可证.
,命题可证.解:(1) 由已知得an+1=an+1,则an+1-an=1,又a1=1,
所以数列{an}是以1为首项,1为公差的等差数列,
故an=1+(n-1)1=n. 4分
(2)由(1)知,an=n,从而
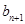 -
-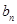 =2n.
=2n.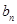 =(
=(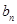 -
- )+(
)+( -
- )+ +(b2-b1)+b1 ,
)+ +(b2-b1)+b1 ,=2n-1+2n-2+ +2+1=
 =
= -1.
-1.因为
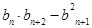 =(2n-1)(2n+2-1)-(2n+1-1)2
=(2n-1)(2n+2-1)-(2n+1-1)2 =(22n+2-2n+2-2n+1)-(22n+2-2·2n+1+1),
=
 <0,
<0,所以
 . 12分
. 12分
练习册系列答案
相关题目
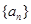 中,
中,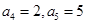 ,则数列
,则数列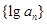 的前8项和等于
的前8项和等于 满足
满足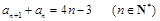 .
.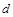 的值;
的值;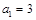 ,求数列
,求数列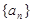 中,
中,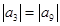 公差
公差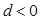 ,那么使
,那么使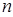 项和
项和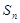 最大的
最大的


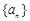 的前
的前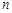 项和
项和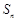 满足
满足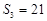 ,
,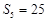 .
.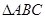 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线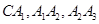 是分别以
是分别以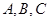 为圆心,
为圆心,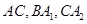 为半径画的弧,曲线
为半径画的弧,曲线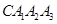 记为螺旋线旋第一圈.然后又以
记为螺旋线旋第一圈.然后又以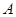 为圆心
为圆心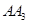 为半径画弧,
为半径画弧,
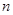 圈,则所得螺旋线的长度
圈,则所得螺旋线的长度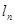 为( )
为( )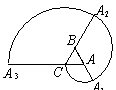

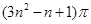


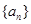 的前
的前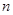 项和为
项和为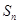 ,若
,若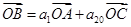 ,且
,且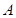 ,
,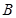 ,
,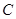 三点共线(该
三点共线(该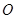 ),则
),则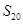 =_____________.
=_____________.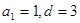 确定的等差数列
确定的等差数列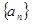 ,当
,当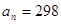 时,序号
时,序号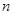 等于( )
等于( )