题目内容
已知数列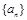 满足
满足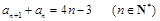 .
.
(1)若数列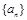 是等差数列,求其公差
是等差数列,求其公差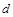 的值;
的值;
(2)若数列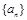 的首项
的首项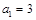 ,求数列
,求数列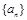 的前100项的和.
的前100项的和.
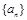 满足
满足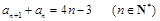 .
.(1)若数列
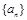 是等差数列,求其公差
是等差数列,求其公差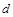 的值;
的值;(2)若数列
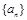 的首项
的首项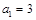 ,求数列
,求数列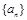 的前100项的和.
的前100项的和.(1)2;(2)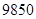
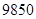
试题分析:(1)设
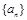 的首项为
的首项为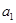 和公差为
和公差为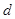 ,则
,则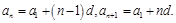 代入已知条件,利用待定系数法可得关于
代入已知条件,利用待定系数法可得关于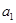 、
、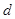 的方程;(2)通过赋值作差可得
的方程;(2)通过赋值作差可得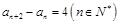 ,然后确定数列的类型,进行分组求和。
,然后确定数列的类型,进行分组求和。(1)因为数列
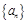 是等差数列,
是等差数列,所以
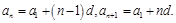 1′
1′由
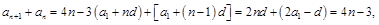 2′
2′所以
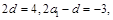 解得
解得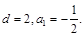
故其公差
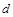 的值为2. 5′
的值为2. 5′(2)由
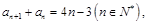 得
得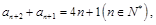
两式相减,得
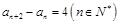 . 6′
. 6′所以数列
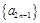 是首项为
是首项为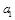 ,公差为4的等差数列; 7′
,公差为4的等差数列; 7′数列
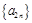 是首项为
是首项为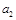 ,公差为4的等差数列. 8′
,公差为4的等差数列. 8′又由
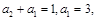 得
得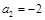 .
.所以
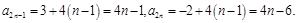
故所求
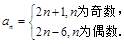 11′
11′所以数列
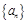 的前100项的和为
的前100项的和为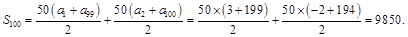 13′
13′
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
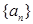 满足
满足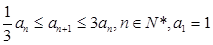 .
.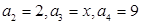 ,求
,求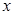 的取值范围;
的取值范围;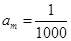 ,正整数
,正整数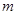 的最小值,以及
的最小值,以及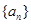 的仅比;
的仅比;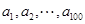 成等差数列,求数列
成等差数列,求数列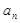 }的前
}的前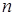 项和为
项和为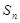 ,且满足
,且满足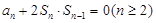 ,
,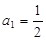 .
.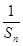 }是等差数列;
}是等差数列;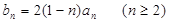 ,求证:
,求证: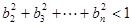 .
.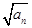 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上. 满足b1=1,
满足b1=1,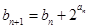 ,求证:
,求证: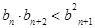 .
.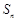 是等差数列
是等差数列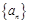 的前
的前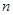 项和,且
项和,且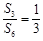 ,则
,则 .
.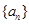 是等差数列,且
是等差数列,且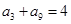 ,那么数列
,那么数列