题目内容
7.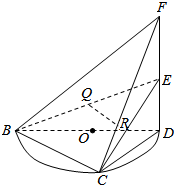 如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.
如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.(Ⅰ)求证:面BCE⊥面CDF;
(Ⅱ)求证:QR∥平面BCD;
(Ⅲ)求三棱锥F-BCE的体积.
分析 (Ⅰ)证明BD⊥DF,DF⊥BC,利用直线与平面垂直的判定定理证明BC⊥平面CFD,然后证明面BCE⊥面CDF.
(Ⅱ)连接OQ,通过证明RQ∥OM,然后证明QR∥平面BCD.
(Ⅲ)利用vF-BCE=vF-BCD-vE-BCD求解几何体的体积即可.
解答 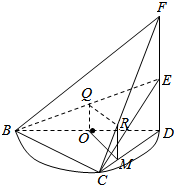 (本小题满分12分)
(本小题满分12分)
证明:(Ⅰ)∵DF=2,$BF=2\sqrt{3}$,$BD=2\sqrt{2}$,∴BF2=BD2+DF2,
∴BD⊥DF----------------------(1分)
又DF⊥CD,∴DF⊥平面BCD----------------------(2分)
∴DF⊥BC,
又BC⊥CD,∴BC⊥平面CFD,----------------------(3分)
∵BC?面BCE
∴面BCE⊥面CDF.----------------------(4分)
(Ⅱ)连接OQ,在面CFD内过R点做RM⊥CD,
∵O,Q为中点,∴OQ∥DF,且$OQ=\frac{1}{2}DE$-----------------(5分)
∵DF⊥CD∴RM∥FD,----------------------(6分)
又FR=3RC,∴$\frac{RM}{DF}=\frac{CR}{CF}=\frac{1}{4}$,∴$RM=\frac{1}{4}DF$,
∵E为FD的中点,∴$RM=\frac{1}{2}DE$.----------------------(7分)
∴OQ∥RM,且OQ=RM
∴OQRM为平行四边形,∵RQ∥OM----------------------(8分)
又RQ?平面BCD,OM?平面BCD,∴QR∥平面BCD.---------------------(9分)
(Ⅲ)∵$\widehat{BC}=2\widehat{CD}$,∴∠DBC=30°,∴在直角三角形BCD中有$CD=\sqrt{2}$,$BC=\sqrt{6}$,
∴${v_{F-BCE}}={v_{F-BCD}}-{v_{E-BCD}}=\frac{1}{3}×\frac{1}{2}×\sqrt{6}×\sqrt{2}×2-\frac{1}{3}×\frac{1}{2}×\sqrt{6}×\sqrt{2}×1=\frac{{\sqrt{3}}}{3}$--------(12分)
点评 本题考查直线与平面垂直的判定定理的应用直线与平面平行的判定定理以及几何体的体积的求法,考查空间想象能力以及逻辑推理计算能力.

| 类别 | A | B | C |
| 数量 | 4 | 3 | 2 |
(Ⅰ)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(Ⅱ)若一次性提取4辆车,其中A,B,C三种型号的车辆数分别记为a,b,c,记ξ为a,b,c的最大值,求ξ的分布列和数学期望.
 如图,在五面体ABCDEF中,AB∥CD∥EF,CD=EF=CF=2AB=2AD=2,∠DCF=60°,AD⊥CD,平面CDEF⊥平面ABCD.
如图,在五面体ABCDEF中,AB∥CD∥EF,CD=EF=CF=2AB=2AD=2,∠DCF=60°,AD⊥CD,平面CDEF⊥平面ABCD. 已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.
已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.