题目内容
4.设n=${∫}_{1}^{2}$$\frac{{x}^{2}-1}{x}$dx,则${e^{n-\frac{3}{2}}}$=$\frac{1}{2}$.分析 根据微积分基本定理求出n的值,再根据对数函数的运算性质即可得到答案.
解答 解:n=${∫}_{1}^{2}$$\frac{{x}^{2}-1}{x}$dx=${∫}_{1}^{2}$(x-$\frac{1}{x}$)dx=($\frac{1}{2}$x2-lnx)|${\;}_{1}^{2}$=$\frac{3}{2}$-ln2,
∴${e^{n-\frac{3}{2}}}$=e-ln2=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了定积分的计算和对数函数的运算性质,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
12.已知复数z满足z(1+i)3=1-i,则复数z对应的点在( )上.
| A. | 直线y=-$\frac{1}{2}$x | B. | 直线y=$\frac{1}{2}$x | C. | 直线x=-$\frac{1}{2}$ | D. | 直线 y=-$\frac{1}{2}$ |
19.一个几何体的三视图如图所示,其中俯视图为正方形及其一条对角线,则该几何体的体积为( )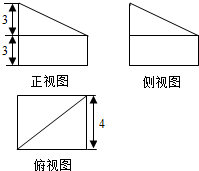

| A. | 32 | B. | 48 | C. | 56 | D. | 96 |
16.已知圆的方程为x2+y2-2x-6y+1=0,那么圆心坐标为( )
| A. | (-1,-3) | B. | (1,-3) | C. | (1,3) | D. | (-1,3) |
14.已知α是第四象限角,且tanα=-$\frac{3}{4}$,则sinα=( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |