题目内容
14.已知α是第四象限角,且tanα=-$\frac{3}{4}$,则sinα=( )| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
分析 由条件利用同角三角函数的基本关系,以及三角函数在各个象限中的符号,求得sinα的值.
解答 解:∵α是第四象限角,且tanα=-$\frac{3}{4}$,
∴sinα<0,$\frac{sinα}{cosα}$=-$\frac{3}{4}$,sin2α+cos2α=1,
求得sinα=-$\frac{3}{5}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
5.已知执行如图所示的程序框图,输出的S=485,则判断框内的条件可以是( )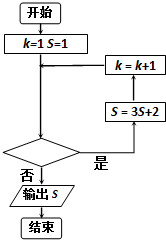

| A. | k<5? | B. | k>7? | C. | k≤5? | D. | k≤6? |
2.已知双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,斜率为$\sqrt{3}$的直线l经过双曲线Γ的右焦点F2与双曲线Γ在第一象限交于点,若△PF1F2是等腰三角形,则双曲线Γ的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |