题目内容
15.若△ABC满足(2$\overrightarrow{CA}$-$\overrightarrow{CB}$)•($\overrightarrow{CA}$-2$\overrightarrow{CB}$)=0,且|$\overrightarrow{AB}$|=2,则|$\overrightarrow{CA}$+$\overrightarrow{CB}$|=6.分析 将已知等式展开,结合|$\overrightarrow{AB}$|=2化为|$\overrightarrow{CB}-\overrightarrow{CA}$|=2得到$\overrightarrow{CA}$•$\overrightarrow{CB}$=8,将所求平方展开,得到所求.
解答 解:(2$\overrightarrow{CA}$-$\overrightarrow{CB}$)•($\overrightarrow{CA}$-2$\overrightarrow{CB}$)=0展开得2${\overrightarrow{CA}}^{2}+2{\overrightarrow{CB}}^{2}-5\overrightarrow{CA}•\overrightarrow{CB}=0$,①
又|$\overrightarrow{AB}$|=2,即|$\overrightarrow{CB}-\overrightarrow{CA}$|=2,平方得${\overrightarrow{CB}}^{2}+{\overrightarrow{CA}}^{2}-2\overrightarrow{CB}•\overrightarrow{CA}=4$②,
由①②可得$\overrightarrow{CA}$•$\overrightarrow{CB}$=8,
所以|$\overrightarrow{CA}$+$\overrightarrow{CB}$|2=|$\overrightarrow{CB}$-$\overrightarrow{CA}$|2+4$\overrightarrow{CA}$•$\overrightarrow{CB}$=4+32=36,
所以|$\overrightarrow{CA}$+$\overrightarrow{CB}$|=6.
故答案为:6.
点评 本题考查了向量的数量积运算以及向量的模的求法;一般的,要求向量的模,先求向量的平方.

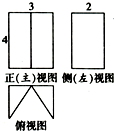
| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
| A. | A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ | B. | C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | ||
| C. | C${\;}_{7}^{3}$--C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | D. | A${\;}_{7}^{3}$--A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ |
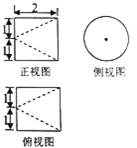
| A. | $\frac{π}{3}$cm3 | B. | $\frac{2π}{3}$cm3 | C. | πcm3 | D. | $\frac{4π}{3}$cm3 |
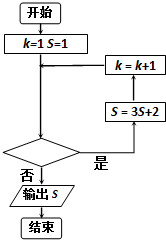
| A. | k<5? | B. | k>7? | C. | k≤5? | D. | k≤6? |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2)则f(x)=2sin($\frac{1}{2}$x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2)则f(x)=2sin($\frac{1}{2}$x+$\frac{π}{6}$).