题目内容
已知椭圆 ,能否在椭圆上位于
,能否在椭圆上位于 轴左侧的部分找到一点
轴左侧的部分找到一点 ,使其到左准线
,使其到左准线 的距离
的距离 为点
为点 到两个焦点
到两个焦点 的距离的等比中项?说明理由。
的距离的等比中项?说明理由。
 ,能否在椭圆上位于
,能否在椭圆上位于 轴左侧的部分找到一点
轴左侧的部分找到一点 ,使其到左准线
,使其到左准线 的距离
的距离 为点
为点 到两个焦点
到两个焦点 的距离的等比中项?说明理由。
的距离的等比中项?说明理由。符合条件的点不存在
∵ ,
, ,左准线
,左准线 ,假设存在
,假设存在
 满足
满足 ,∵
,∵ ,
, ,
, ,又
,又 ,∴
,∴ ,解得
,解得 ,与
,与 矛盾,假设不成立,故这样的符合条件的点不存在。
矛盾,假设不成立,故这样的符合条件的点不存在。
 ,
, ,左准线
,左准线 ,假设存在
,假设存在
 满足
满足 ,∵
,∵ ,
, ,
, ,又
,又 ,∴
,∴ ,解得
,解得 ,与
,与 矛盾,假设不成立,故这样的符合条件的点不存在。
矛盾,假设不成立,故这样的符合条件的点不存在。
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
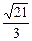 的双曲线过点P(6,6).
的双曲线过点P(6,6). 的焦距为
的焦距为 ,则
,则 的值为( )
的值为( )


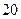




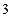 倍,且过点
倍,且过点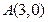 ,并且以坐标轴为对称轴,
,并且以坐标轴为对称轴,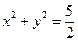 ;②
;②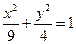 ;③
;③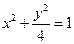 ;④
;④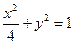 。其中与直线
。其中与直线 仅有一个交点的直线是( )
仅有一个交点的直线是( ) 的左、右焦点,O为坐标原点,以
的左、右焦点,O为坐标原点,以 为半径的圆与该左半椭圆的两个交点A、B,且
为半径的圆与该左半椭圆的两个交点A、B,且 是等边三角形,则椭圆的离心率为( )
是等边三角形,则椭圆的离心率为( ) B.
B.  C.
C. D.
D. 
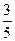 ,一条准线的方程为
,一条准线的方程为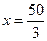 ,求椭圆的标准方程。
,求椭圆的标准方程。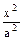 +
+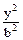 =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,求椭圆的离心率
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,求椭圆的离心率