题目内容
已知数列 的前三项分别为
的前三项分别为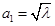 ,
,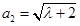 ,
,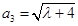 ,(其中
,(其中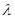 为正常数)。设
为正常数)。设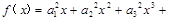
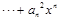 。
。
(1)归纳出数列 的通项公式,并证明数列
的通项公式,并证明数列 不可能为等比数列;
不可能为等比数列;
(2)若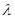 =1,求
=1,求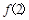 的值;
的值;
(3)若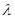 =4,试证明:当
=4,试证明:当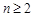 时,
时,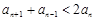 .
.
 的前三项分别为
的前三项分别为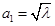 ,
,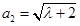 ,
,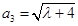 ,(其中
,(其中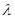 为正常数)。设
为正常数)。设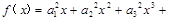
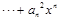 。
。(1)归纳出数列
 的通项公式,并证明数列
的通项公式,并证明数列 不可能为等比数列;
不可能为等比数列;(2)若
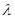 =1,求
=1,求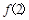 的值;
的值;(3)若
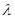 =4,试证明:当
=4,试证明:当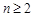 时,
时,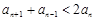 .
.(1)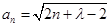 ,证明详见解析;(2)
,证明详见解析;(2)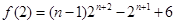 ;(3)详见解析.
;(3)详见解析.
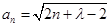 ,证明详见解析;(2)
,证明详见解析;(2)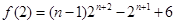 ;(3)详见解析.
;(3)详见解析.试题分析:(1)根据条件中给出的
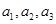 的表达式,可以归纳出数列
的表达式,可以归纳出数列 的通项公式为
的通项公式为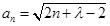 ,证明
,证明 不可能为等比数列可以考虑采用反证法来证明,假设
不可能为等比数列可以考虑采用反证法来证明,假设 为等比数列,可以得到与事实不符的等式,从而得证;(2)若
为等比数列,可以得到与事实不符的等式,从而得证;(2)若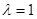 时,
时, 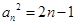 ∴
∴ ,
,∴
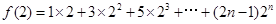 ,利用错位相减法进行数列求和,即可得到f(2)的表达式;(3)当
,利用错位相减法进行数列求和,即可得到f(2)的表达式;(3)当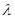 =4,欲证当
=4,欲证当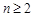 时,
时,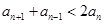 ,即证
,即证 ,尝试采用分析法,从要证明的不等式出发,执果索因,即可得证
,尝试采用分析法,从要证明的不等式出发,执果索因,即可得证(1)数列
 的通项公式为
的通项公式为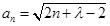 2分
2分下面证明数列
 不可能为等比数列:
不可能为等比数列:假设数列
 为等比数列,则
为等比数列,则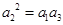 ,即
,即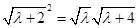 (
(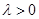 ),
),即
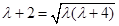 ,两边平方整理得:4=0,矛盾,
,两边平方整理得:4=0,矛盾,故数列
 不可能为等比数列 5分
不可能为等比数列 5分(2)若
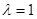 ,
,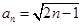 ,∴
,∴ 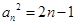 ,∴
,∴ ,
,
∴
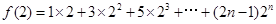 ①
①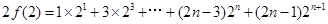 ②
②①-②得
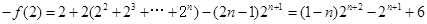
∴
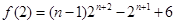 9分
9分(3)若
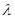 =4,
=4,
法一:当
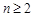 时,欲证
时,欲证 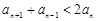 ,
,只需证

只需证
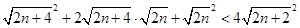
只需证
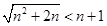
只需证
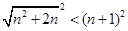
只需证

显然 不等式
 成立,
成立,因此 当
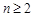 时,
时,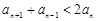 . 14分
. 14分法二:
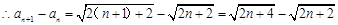
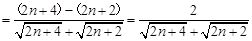

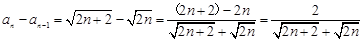
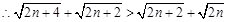 ,
,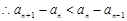 ,
,故
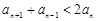 .
. 
练习册系列答案
相关题目
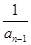 (n≥2,n∈N*).
(n≥2,n∈N*).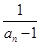 ,n∈N*,求证:数列{bn}是等差数列;
,n∈N*,求证:数列{bn}是等差数列;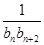 (n∈N*),求数列{cn}的前n项和Sn.
(n∈N*),求数列{cn}的前n项和Sn.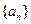 的公差大于零的等差数列,已知
的公差大于零的等差数列,已知 ,
, .
. 是以函数
是以函数 的最小正周期为首项,以
的最小正周期为首项,以 为公比的等比数列,求数列
为公比的等比数列,求数列 的前
的前 项和
项和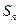 .
. 满足
满足 则
则 .
. }是等差数列,数列{
}是等差数列,数列{ }的前
}的前 项和
项和 满足
满足 ,
, ,
, 。
。 为数列{
为数列{ 满足
满足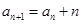 +1,且
+1,且 ,则
,则
 =( ).
=( ).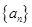 的首项
的首项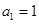 ,公差
,公差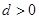 ,数列
,数列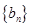 是等比数列,且
是等比数列,且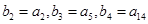 .
.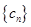 对任意正整数n,均有
对任意正整数n,均有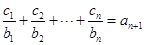 成立,求
成立,求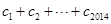 的值.
的值.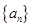 的前
的前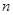 项和为
项和为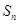 ,若
,若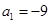 ,且
,且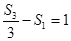 ,则
,则