题目内容
设数列{ }是等差数列,数列{
}是等差数列,数列{ }的前
}的前 项和
项和 满足
满足 ,
, ,
,
且 。
。
(1)求数列{ }和{
}和{ }的通项公式:
}的通项公式:
(2)设 为数列{
为数列{ .
. }的前
}的前 项和,求
项和,求 .
.
 }是等差数列,数列{
}是等差数列,数列{ }的前
}的前 项和
项和 满足
满足 ,
, ,
,且
 。
。(1)求数列{
 }和{
}和{ }的通项公式:
}的通项公式:(2)设
 为数列{
为数列{ .
. }的前
}的前 项和,求
项和,求 .
.(1)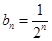 ;
;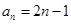 (2)
(2)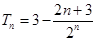
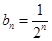 ;
;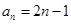 (2)
(2)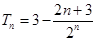
试题分析:(1)根据公式
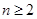 时,
时,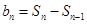 可推导出
可推导出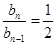 ,根据等比数列的定义可知数列
,根据等比数列的定义可知数列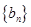 是公比为
是公比为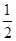 的等比数列,由等比数列的通项公式
的等比数列,由等比数列的通项公式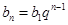 可求
可求 。从而可得
。从而可得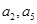 的值。由
的值。由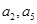 的值可得公差
的值可得公差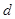 ,从而可得首项
,从而可得首项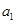 。根据等差数列的通项公式
。根据等差数列的通项公式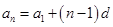 可得
可得 。(2)用错位相减法求数列的和
。(2)用错位相减法求数列的和 :先将
:先将 的式子列出,然后左右两边同乘以等比数列
的式子列出,然后左右两边同乘以等比数列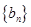 的公比
的公比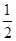 ,并将等式右边空出一个位置,然后将两个式子相减,用等比数列的前
,并将等式右边空出一个位置,然后将两个式子相减,用等比数列的前 项和公式整理计算,可得
项和公式整理计算,可得 。
。解(1)由
 (1)
(1)知当
 =1时,
=1时,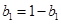 ,
, 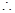
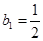 .
.当

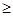 2时,
2时,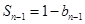 (2)
(2)(1)
 (2)得
(2)得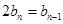 ,
, 
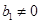
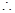
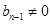
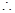
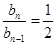 (
(
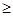 2)
2) 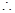
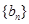 是以
是以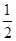 为首项以
为首项以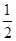 为公比的等比数列,
为公比的等比数列,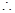
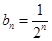
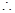
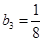 4分
4分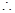
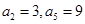
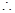
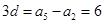
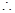
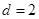
故
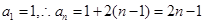 . 6分
. 6分(2)
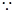
 .
. =
=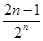 . 7
. 7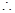
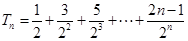 ①
①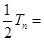
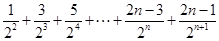 ②
②①
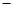 ②得
②得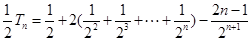
=
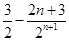 . 11分
. 11分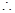
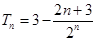 . 12分
. 12分
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
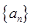 中,其前
中,其前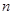 项和为
项和为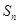 ,且
,且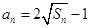 .
.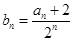 ,
,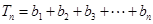 ,求证:
,求证: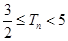 ;
;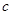 为实数,对任意满足成等差数列的三个不等正整数
为实数,对任意满足成等差数列的三个不等正整数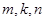 ,不等式
,不等式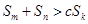 都成立,求实数
都成立,求实数 的前三项分别为
的前三项分别为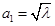 ,
,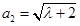 ,
,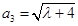 ,(其中
,(其中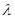 为正常数)。设
为正常数)。设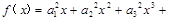
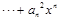 。
。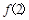 的值;
的值;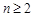 时,
时,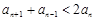 .
.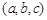 ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果 ,可实施如下操作
,可实施如下操作 :若
:若 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若 ,其级差为
,其级差为 .若
.若 ,则继续对
,则继续对 ,…,实施
,…,实施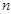 次操作后的结果记为
次操作后的结果记为 ,其极差记为
,其极差记为 .例如:
.例如: ,
,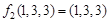 .
. ,求
,求 和
和 的值;
的值; 的极差为
的极差为 且
且 ,若
,若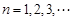 时,恒有
时,恒有 ,求
,求 的所有可能取值;
的所有可能取值;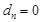 .
.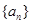 满足:
满足: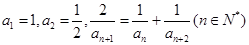 .
.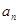 ;
;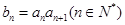 ,求数列
,求数列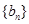 的前
的前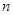 和
和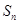 .
.



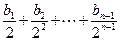 ,an=
,an=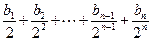 (
(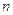 为正整数),
为正整数),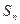 ,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn, }的通项公式为
}的通项公式为 ,那么
,那么 是它的第_ __项.
是它的第_ __项.