题目内容
已知数列{an}中,a1=2,an=2-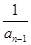 (n≥2,n∈N*).
(n≥2,n∈N*).
(1)设bn=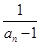 ,n∈N*,求证:数列{bn}是等差数列;
,n∈N*,求证:数列{bn}是等差数列;
(2)设cn=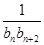 (n∈N*),求数列{cn}的前n项和Sn.
(n∈N*),求数列{cn}的前n项和Sn.
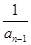 (n≥2,n∈N*).
(n≥2,n∈N*).(1)设bn=
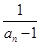 ,n∈N*,求证:数列{bn}是等差数列;
,n∈N*,求证:数列{bn}是等差数列;(2)设cn=
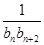 (n∈N*),求数列{cn}的前n项和Sn.
(n∈N*),求数列{cn}的前n项和Sn.(1)见解析 (2)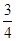 -
-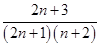
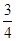 -
-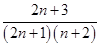
(1)证明 ∵an=2-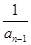 ,∴an+1=2-
,∴an+1=2-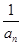 .
.
∴bn+1-bn=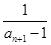 -
-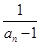 =
=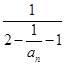 -
-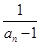 =
=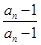 =1,
=1,
∴{bn}是首项为b1=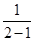 =1,公差为1的等差数列.
=1,公差为1的等差数列.
(2)解 由(1)知bn=n,
∴cn=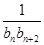 =
=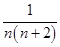 =
=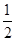 (
(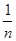 -
-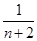 ),
),
∴Sn=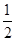 [(1-
[(1-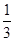 )+(
)+(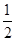 -
-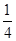 )+(
)+(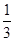 -
-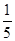 )+…+(
)+…+(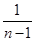 -
-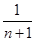 )+(
)+(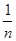 -
-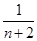 )]
)]
=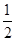 (1+
(1+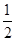 -
-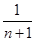 -
-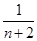 )=
)=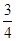 -
-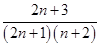 .
.
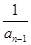 ,∴an+1=2-
,∴an+1=2-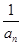 .
.∴bn+1-bn=
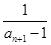 -
-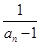 =
=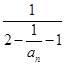 -
-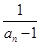 =
=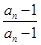 =1,
=1,∴{bn}是首项为b1=
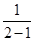 =1,公差为1的等差数列.
=1,公差为1的等差数列.(2)解 由(1)知bn=n,
∴cn=
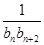 =
=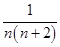 =
=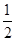 (
(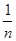 -
-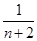 ),
),∴Sn=
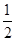 [(1-
[(1-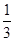 )+(
)+(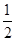 -
-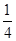 )+(
)+(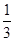 -
-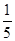 )+…+(
)+…+(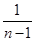 -
-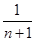 )+(
)+(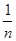 -
-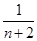 )]
)]=
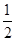 (1+
(1+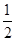 -
-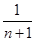 -
-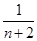 )=
)=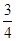 -
-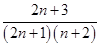 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前三项分别为
的前三项分别为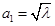 ,
,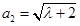 ,
,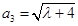 ,(其中
,(其中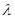 为正常数)。设
为正常数)。设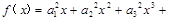
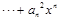 。
。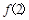 的值;
的值;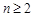 时,
时,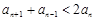 .
.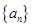 满足
满足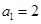 ,向量
,向量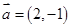 ,
,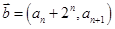 且
且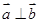 .
.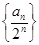 为等差数列,并求
为等差数列,并求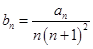 ,若对任意
,若对任意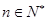 都有
都有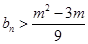 成立,求实数
成立,求实数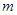 的取值范围.
的取值范围.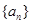 满足:
满足: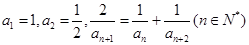 .
.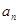 ;
;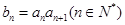 ,求数列
,求数列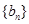 的前
的前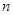 和
和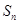 .
.



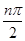 -bn·cos2
-bn·cos2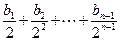 ,an=
,an=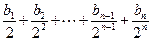 (
(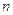 为正整数),
为正整数),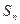 ,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,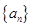 ,
,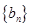 的前
的前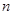 项和分别为
项和分别为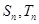 ,若
,若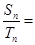
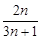 ,则
,则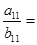 _________.
_________.