题目内容
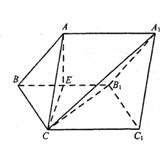
【题目】如图,在正四棱锥![]() 中,
中,![]() ,
,![]() .
.
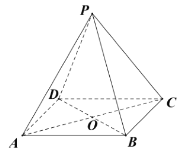
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)![]() 为正四棱锥.所以
为正四棱锥.所以![]() 为正方形,
为正方形,![]() 面
面![]() ,
,![]() .
.
因为![]() 为正方形,所以
为正方形,所以![]() .
. ![]() ,所以
,所以![]() 面
面![]() .
.
(2)要求二面角![]() 的余弦值,通过建立空间直角坐标系,运用向量法即可得出答案.
的余弦值,通过建立空间直角坐标系,运用向量法即可得出答案.
(1)证明:联结![]() .
.
在正四棱锥![]() 中,
中,![]() 底面
底面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
在正方形![]() 中,
中,![]() ,
,
又因为![]() ,所以
,所以![]() 面
面![]() .
.
(2)解:由(1)知,![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
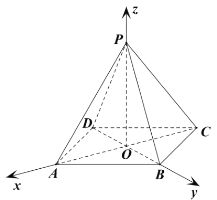
以![]() 为坐标原点建立如图所示空间直角坐标系.
为坐标原点建立如图所示空间直角坐标系.
在正方形![]() 中,因为
中,因为![]() ,
,
所以![]() .
.
又因为![]() ,
,
所以![]() .
.
所以点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
点![]() 的坐标为
的坐标为![]() .
.
则![]() ,
,![]() .
.
由(1)知,![]() 平面
平面![]() .
.
所以平面![]() 的一个法向量为
的一个法向量为![]() . 设平面
. 设平面![]() 的一个法向量
的一个法向量![]() .
.
则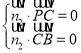 ,即
,即![]()
令![]() ,则
,则![]() ,
,![]() .
.
故平面![]() 的一个法向量
的一个法向量![]() .
. 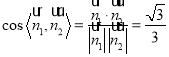
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某省级示范高中高三年级对各科考试的评价指标中,有“难度系数“和“区分度“两个指标中,难度系数![]() ,区分度
,区分度![]() .
.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147,142,137;普通班三人的成绩分别为97,102,113.通过样本估计本次考试的区分度(精确0.01).
(2)如表表格是该校高三年级6次数学考试的统计数据:
难度系数x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
区分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①计算相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y关于t的线性回归方程,并预测x=0.75时y的值(精确到0.01).
附注:参考数据: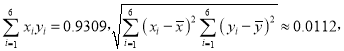
![]()
![]()
参考公式:相关系数 r,回归直线
r,回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
【题目】某市组织高三全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
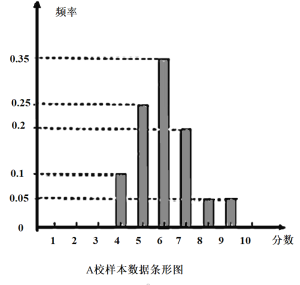
B校样本数据统计表:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.