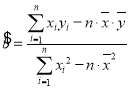题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(2)设![]() ,当
,当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)先求导函数,求出f'(x)=0的根,然后比较根与区间的关系,确定a的范围,根据f'(x)>0的解集为增区间,f'(x)<0的解集为减区间求解即可;
(2)先证得![]() 恒成立,再将h(x)通过
恒成立,再将h(x)通过![]() 进行放缩,得到
进行放缩,得到![]() ,构造函数L(x),求导分析单调性、极值,从而求得最小值,可证得结论.
,构造函数L(x),求导分析单调性、极值,从而求得最小值,可证得结论.
(1)![]()
![]() ,
,![]()
![]() ,
,
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 恒成立,
恒成立,
![]()
![]() 在
在![]() 上的单调递增;
上的单调递增;
∴当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() ,
,![]()
![]() 在
在![]() 上单调递减;
上单调递减;
∴当![]() 时,
时,![]() ,
,![]()
![]() 在
在![]() 上单调递增.
上单调递增.
综上,当![]() 时,
时, ![]() 在
在![]() 上的单调递增;
上的单调递增;
当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)令![]() ,得
,得![]() ,
,![]()
![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]()
![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]()
![]() 在
在![]() 上单调递增;
上单调递增;
![]()
![]() ,即
,即![]() .
.
当![]() 时,
时,
![]()
![]()
![]() ,
,
当且仅当![]() 时取等号,
时取等号,
令![]() ,则
,则![]() .
.
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
易知此不等式中两等号成立的条件不同,![]()
![]()

【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
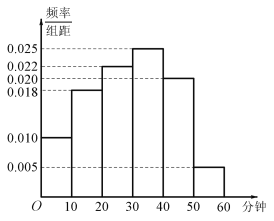
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的2×2列联表;
(2)根据此资料,判断是否有![]() 的把握认为“体育迷”与性别有关?
的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
附: ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】现有某高新技术企业年研发费用投入![]() (百万元)与企业年利润
(百万元)与企业年利润![]() (百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
(百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
年研发费用 |
|
|
|
|
|
年利润 |
|
|
|
|
|
数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(1)求![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考数据:回归直线的系数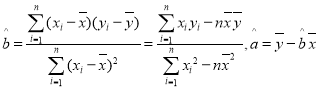 .
.
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如下表所示:
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 23 | 30 | |
女 | 11 | ||
总计 | 50 |
表(1)
并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如下表(2)所示.
成功完成时间(分钟) |
|
|
|
|
人数 | 10 | 4 | 4 | 2 |
表(2)
(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表(2)中成功完成时间在![]() 和
和![]() 这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
附参考公式及参考数据:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |