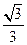题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,短轴一个端点到右焦点的距离为
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,以AB弦为直径的圆过坐标原点O,试探讨点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 3 |
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,以AB弦为直径的圆过坐标原点O,试探讨点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由.
(1)设椭圆的半焦距为c,依题意
∴b=1,….(2分)
∴所求椭圆方程为
+y2=1.…..(4分)
(2)设A(x1,y1),B(x2,y2).
①当AB⊥x轴时,设AB方程为:x=m,此时A,B两点关于x轴对称,又以|AB|为直径的圆过原点,
设A(m,m)代入椭圆方程得:m=
….(6分)
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.联立
,
整理得(3k2+1)x2+6kmx+3m2-3=0,∴x1+x2=
,x1x2=
.….(8分)
又y1y2=k2x1x2+km(x1+x2)+m2=
+
+m2=
.
由以|AB|为直径的圆过原点,则有
•
=0.…..(10分)
即:x1x2+y1y2=0,故满足:
+
=0得:4m2=3+3k2,所以m2=
(k2+1).
又点O到直线AB的距离为:d=
=
=
.
综上所述:点O到直线AB的距离为定值
.…(13分)
|
∴所求椭圆方程为
| x2 |
| 3 |
(2)设A(x1,y1),B(x2,y2).
①当AB⊥x轴时,设AB方程为:x=m,此时A,B两点关于x轴对称,又以|AB|为直径的圆过原点,
设A(m,m)代入椭圆方程得:m=
| ||
| 2 |
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.联立
|
整理得(3k2+1)x2+6kmx+3m2-3=0,∴x1+x2=
| -6km |
| 3k2+1 |
| 3(m2-1) |
| 3k2+1 |
又y1y2=k2x1x2+km(x1+x2)+m2=
| 3k2(m2-1) |
| 1+3k2 |
| -6k2m2 |
| 1+3k2 |
| m2-3k2 |
| 1+3k2 |
由以|AB|为直径的圆过原点,则有
| OA |
| OB |
即:x1x2+y1y2=0,故满足:
| 3(m2-1) |
| 1+3k2 |
| m2-3k2 |
| 1+3k2 |
| 3 |
| 4 |
又点O到直线AB的距离为:d=
| |m| | ||
|
| ||||||
|
| ||
| 2 |
综上所述:点O到直线AB的距离为定值
| ||
| 2 |

练习册系列答案
相关题目

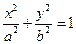
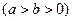 的左、右焦点分别为
的左、右焦点分别为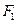 、
、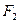 ,抛物线
,抛物线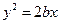 的焦点为
的焦点为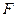 .若
.若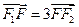 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )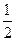 B.
B.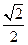 C.
C.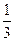 D.
D.