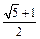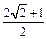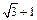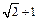题目内容
设椭圆C:
+
=1(a>b>0)过点(1,
),F1,F2分别为椭圆C的左右焦点,且离心率e=
(1)求椭圆C的方程.
(2)已知A为椭圆C的左顶点,直线l过右焦点F2与椭圆C交于M,N两点,若AM、AN的斜率k1,k2满足k1+k2=-
,求直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
(1)求椭圆C的方程.
(2)已知A为椭圆C的左顶点,直线l过右焦点F2与椭圆C交于M,N两点,若AM、AN的斜率k1,k2满足k1+k2=-
| 1 |
| 2 |
(1)∵椭圆C:
+
=1(a>b>0)过点(1,
),且离心率e=
,∴
,解得
,∴椭圆C的方程为
+
=1.
(2)由(1)可得:左顶点A(-2,0),右焦点(1,0).
由题意可知直线l不存在时不满足条件,可设直线l的方程为y=k(x-1),M(x1,y1),N(x2,y2).
联立
,化为(3+4k2)x2-8k2x+4k2-12=0.由题意可得△>0.
∴x1+x2=
,x1x2=
.
∵k1+k2=-
,∴
+
=-
,
化为2k(x1-1)(x2+2)+2k(x2-1)(x1+2)+(x1+2)(x2+2)=0,
整理为(4k+1)x1x2+(2k+2)(x1+x2)+4-8k=0.
代入得
+
+4-8k=0,
整理为k2-2k=0,解得k=0或2.
k=0不满足题意,应舍去.
故k=2,此时直线l的方程为y=2(x-1),即2x-y-2=0.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
|
|
| x2 |
| 4 |
| y2 |
| 3 |
(2)由(1)可得:左顶点A(-2,0),右焦点(1,0).
由题意可知直线l不存在时不满足条件,可设直线l的方程为y=k(x-1),M(x1,y1),N(x2,y2).
联立
|
∴x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∵k1+k2=-
| 1 |
| 2 |
| y1 |
| x1+2 |
| y2 |
| x2+2 |
| 1 |
| 2 |
化为2k(x1-1)(x2+2)+2k(x2-1)(x1+2)+(x1+2)(x2+2)=0,
整理为(4k+1)x1x2+(2k+2)(x1+x2)+4-8k=0.
代入得
| (4k+1)(4k2-12) |
| 3+4k2 |
| 8k2(2k+2) |
| 3+4k2 |
整理为k2-2k=0,解得k=0或2.
k=0不满足题意,应舍去.
故k=2,此时直线l的方程为y=2(x-1),即2x-y-2=0.

练习册系列答案
相关题目
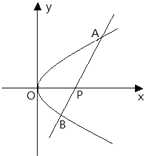
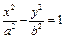 有相同焦点F,点A是两曲线交点,且AF⊥x轴,则双曲线的离心率为 ( )
有相同焦点F,点A是两曲线交点,且AF⊥x轴,则双曲线的离心率为 ( )