Question

13．已知实数x，y满足不等式组$\left\{\begin{array}{l}{xy≥0}\\{|x+y|≤1}\end{array}\right.$，则该不等式组表示的平面区域的面积为1，若目标函数z₁=ax+y取得最大值的最优解有2个，则目标函数z₁=ax+y+3的最小值是2．

Answer 1

分析 作出不等式组对应的平面区域，求出平面区域的面积，利用z=ax+y取得最大值的最优解有2个，利用数形结合确定a的取值即可得到结论．

解答 解：不等式组$\left\{\begin{array}{l}{xy≥0}\\{|x+y|≤1}\end{array}\right.$，等价为$\left\{\begin{array}{l}{x≥0，y≥0}\\{x+y≤1}\end{array}\right.$或$\left\{\begin{array}{l}{x≤0，y≤0}\\{-x-y≤1}\end{array}\right.$，
作出不等式组对应的平面区域如图：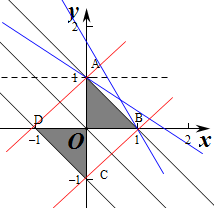
则平面区域为两个相同的直角三角形，则S=2×$\frac{1}{2}×1×1$=1．
由z=ax+y得y=-ax+z，
若a=0时，直线y=-ax+z=z，此时取得最大值的最优解只有一个，不满足条件．
若-a＞0，则直线y=-ax+z截距取得最大值时，z取的最大值，
此时满足直线y=-ax+z经过点A，D时满足条件，此时-a=1，解得a=-1．
若-a＜0，则直线y=-ax+z截距取得最大值时，z取的最大值，此时z=ax+y取得最大值的最优解有1个或者无数个，不满足条件．
综上满足条件的a=-1，即z=-x+y+3，
则y=x+z-3，当直线y=x+z-3经过B（1，0），C（0，-1）时，目标函数取得最小值，
此时z=-1+0+3=2，
故答案为：1，2

点评 本题主要考查线性规划的应用，利用z的几何意义，结合z=ax+y取得最大值的最优解有2个，利用结合数形结合是解决本题的关键．