题目内容
【题目】若f(x)=x3+ax2+bx+c有两个极值点x1 , x2且f(x1)=x1 , 则关于x的方程3[(f(x)]2+2af(x)+b=0的不同实根个数为( )
A.2
B.3
C.4
D.不确定
【答案】B
【解析】解:∵函数f(x)=x3+ax2+bx+c有两个极值点x1 , x2 , 不妨设x1<x2 , ∴f′(x)=3x2+2ax+b=0有两个不相等的实数根,
∴△=4a2﹣12b>0.解得x= ![]() .
.
∵x1<x2 ,
∴x1= ![]() ,x2=
,x2= ![]() .
.
而方程3(f(x))2+2af(x)+b=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2 .
不妨取0<x1<x2 , f(x1)>0.
①把y=f(x)向下平移x1个单位即可得到y=f(x)﹣x1的图象,
∵f(x1)=x1 , 可知方程f(x)=x1有两解.
②把y=f(x)向下平移x2个单位即可得到y=f(x)﹣x2的图象,
∵f(x1)=x1 , ∴f(x1)﹣x2<0,可知方程f(x)=x2只有一解.
综上①②可知:方程f(x)=x1或f(x)=x2 . 只有3个实数解.
即关于x的方程3(f(x))2+2af(x)+b=0的只有3不同实根.
故选:B.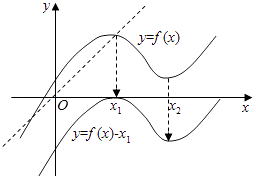
【考点精析】通过灵活运用函数的极值与导数,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目