题目内容
【题目】设a≥0，f（x）=x﹣1﹣ln2x+2alnx（x＞0）． （Ⅰ）令F（x）=xf′（x），讨论F（x）在（0，+∞）内的单调性并求极值；
（Ⅱ）求证：当x＞1时，恒有x＞ln2x﹣2alnx+1．
【答案】解：（Ⅰ）根据求导法则有 
， 故F（x）=xf'（x）=x﹣2lnx+2a，x＞0，
于是 
，
∴知F（x）在（0，2）内是减函数，在（2，+∞）内是增函数，
所以，在x=2处取得极小值F（2）=2﹣2ln2+2a．
（Ⅱ）证明：由a≥0知，F（x）的极小值F（2）=2﹣2ln2+2a＞0．
于是知，对一切x∈（0，+∞），恒有F（x）=xf'（x）＞0．
从而当x＞0时，恒有f'（x）＞0，故f（x）在（0，+∞）内单调增加．
所以当x＞1时，f（x）＞f（1）=0，即x﹣1﹣ln2x+2alnx＞0．
故当x＞1时，恒有x＞ln2x﹣2alnx+1．
【解析】（1）先根据求导法求导数fˊ（x），在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0，求出单调区间及极值即可．（2）欲证x＞ln2x﹣2a ln x+1，即证x﹣1﹣ln2x+2alnx＞0，也就是要证f（x）＞f（1），根据第一问的单调性即可证得．
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数，需要了解一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数的极值的方法是:（1）如果在
附近的左侧
,右侧
,那么
是极大值（2）如果在附近的左侧,右侧
,那么
是极小值才能得出正确答案．
【题目】宿州某中学N名教师参加“低碳节能你我他”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示． 
下表是年龄的频数分布表：
区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
人数 | 25 | m | p | 75 | 25 |
（1）求正整数m，p，N的值；
（2）用分层抽样的方法，从第1、3、5组抽取6人，则第1、3、5组各抽取多少人？
（3）在（2）的条件下，从这6人中随机抽取2人参加学校之间的宣传交流活动，求恰有1人在第3组的概率．
【题目】下表是某厂的产量x与成本y的一组数据：
产量x（千件） | 2 | 3 | 5 | 6 |
成本y（万元） | 7 | 8 | 9 | 12 |
（Ⅰ）根据表中数据，求出回归直线的方程 
= 
x 
（其中 = 
， 
= 
﹣ 
）
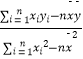（Ⅱ）预计产量为8千件时的成本．