题目内容
【题目】如图所示，在△ABC中，D、F分别是BC、AC的中点， 
= 
， 
= 
， 
= 
． 
（1）用 、 表示向量 
、 、 
、 
、 
；
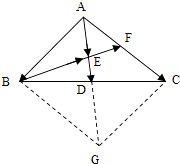
（2）求证：B、E、F三点共线．
【答案】
（1）解：如图所示：解延长AD到G，使 
= 
，
连接BG、CG，得到四边形ABGC，
∵D是BC和AG的中点，
∴四边形ABGC是平行四边形，则 
= 
+ 
= 
，
∴ = = 
（ ）， 
= 
= 
（ ）．
∵F是AC的中点，∴ 
= 
= 
，
∴ 
= ﹣ = （ ）﹣ 
= （ 
）．
= ﹣ = ﹣ = （ ）
（2）证明：由（1）可知， = （ ）， = （ ）．
∴ = 
，即 、 是共线向量，所以B、E、F三点共线
【解析】（1）由题意作出辅助线构成平行四边形ABGC，由四边形法则和D是AG的中点求出 ，由题意求出 ，由F是AC的中点求出 ，再由向量减法的三角形法则求出 和 ；（2）由（1）求出 = ，故两个向量共线，即B、E、F三点共线．
练习册系列答案
相关题目
【题目】下表是某厂的产量x与成本y的一组数据：
产量x（千件） | 2 | 3 | 5 | 6 |
成本y（万元） | 7 | 8 | 9 | 12 |
（Ⅰ）根据表中数据，求出回归直线的方程 
= 
x 
（其中 = 
， 
= 
﹣ 
）
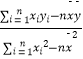（Ⅱ）预计产量为8千件时的成本．
