题目内容
【题目】已知向量 
， 
，若A，B，C是锐角△ABC的三个内角，，则 
与 
的夹角为（ ）
A.锐角
B.直角
C.钝角
D.以上都不对
【答案】A
【解析】解：设 
与 
的夹角为α， ∵向量 
， 
，
∴ =﹣cosAcosB+sinAsinB
=﹣cos（A+B），
而 =| || |cosα
= 
cosα=cosα，
又A和B为锐角△ABC的内角，
∴A+B为钝角，即cos（A+B）＜0，
∴cosα=﹣cos（A+B）=cosC＞0，
则 与 的夹角为锐角．
故选A
【考点精析】掌握数量积表示两个向量的夹角和两角和与差的正弦公式是解答本题的根本，需要知道设
、
都是非零向量，
，
，
是与
的夹角，则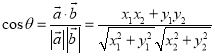
；两角和与差的正弦公式：
．
练习册系列答案
相关题目
【题目】某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如表数据：
单价x（元） | 4 | 5 | 6 | 7 | 8 | 9 |
销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据，求得线性回归方程为 
=﹣4x+a．若在这些样本点中任取一点，则它在回归直线左下方的概率为 （ ）
A.
B.
C.
D.
