题目内容
1.已知f(x)=1-xlnx,g(x)=-x2+2ax(a>0).(1)求函数y=f(x)的单调区间.
(2)若对任意的x2∈[0,1],均存在x1∈[0,+∞),使得f(x1)>g(x2),求a的取值范围.
分析 (1)求导,利用导函数符号判断函数单调区间
(2)有题意知,只需使f(x)的最大值大于g(x)的区间最大值即可.
解答 (1)f′(x)=-(lnx+1),
令f′(x)>0得:0<x<$\frac{1}{e}$,∴f(x)的单调递增区间是(0,$\frac{1}{e}$);
令f′(x)<0得:x>$\frac{1}{e}$,∴f(x)的单调递减区间是( $\frac{1}{e}$,+∞).
(2)g(x)=-x(x-2a),
当a≤1时,g(x)max=g(a)=a2;
由(1)知f(x)max=f($\frac{1}{e}$)=1+$\frac{1}{e}$,
∴1+$\frac{1}{e}$>a2显然成立,
当a>1时,g(x)max=g(1)=-1+2a;
1+$\frac{1}{e}$>-1+2a,
得a<$\frac{2e+1}{2e}$,
故a的范围为0<a<$\frac{2e+1}{2e}$.
点评 考查导函数利用,对存在性的理解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设连续正整数的集合I={10,…,2351}.若T是I的子集且满足条件:当x∈T时,7x∉T,则集合T中元素的个数最多是( )
| A. | 2015 | B. | 2016 | C. | 2054 | D. | 2055 |
9.若tanx=$\sqrt{3}$,且角x∈(-π,π),则x=( )
| A. | -$\frac{2}{3}$π和$\frac{1}{3}$π | B. | -$\frac{1}{3}$π和$\frac{2}{3}$π | C. | -$\frac{5}{6}$π和$\frac{1}{6}$π | D. | -$\frac{1}{6}$π和$\frac{5}{6}$π |
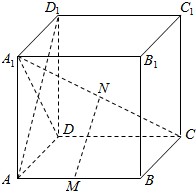 如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证:
如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证: