题目内容
13.已知函数f(x)=$\frac{a}{lo{g}_{a}x}$(a>1)的图象沿着向量$\overrightarrow{a}$=(-2,1)平移后,若在[2,6]中的最大值与最小值的差为$\frac{2a}{3}$,则a的值为16.分析 由题意求出平移后图象所对应的函数解析式,然后利用函数的单调性求出在区间[2,6]中的最大值与最小值,再由最大值与最小值的差为$\frac{2a}{3}$列式求得a的值.
解答 解:把函数f(x)=$\frac{a}{lo{g}_{a}x}$(a>1)的图象沿着向量$\overrightarrow{a}$=(-2,1)平移后,所得函数解析式为,$y=\frac{a}{lo{g}_{a}(x+2)}+1$.
∵在[2,6]上,函数g(x)=loga(x+2)为增函数,且loga(x+2)>0,
∴$y=\frac{a}{lo{g}_{a}(x+2)}+1$ 在[2,6]上为减函数,
则${y}_{max}=\frac{a}{lo{g}_{a}4}+1,{y}_{min}=\frac{a}{lo{g}_{a}8}+1$,
由题意可得:$\frac{a}{lo{g}_{a}4}+1-\frac{a}{lo{g}_{a}8}-1=\frac{2a}{3}$,即$lo{g}_{4}a-lo{g}_{8}a=\frac{2}{3}$,
∴$\frac{1}{6}lo{g}_{2}a=\frac{2}{3}$,解得:a=16.
故答案为:16.
点评 本题考查平面向量坐标表示的应用,考查了函数图象的平移,训练了利用函数的单调性求函数的最值,考查了对数方程的解法,是基础题.

练习册系列答案
相关题目
18.在正方体中,相互平行的面不会是( )
| A. | 前后相对侧面 | B. | 上下相对底面 | C. | 左右相对侧面 | D. | 相邻的侧面 |
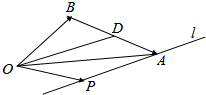 在△OAB中,D是线段AB的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}$=λ1$\overrightarrow{OA}$+λ2$\overrightarrow{OB}$,则λ1-λ2=1.
在△OAB中,D是线段AB的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}$=λ1$\overrightarrow{OA}$+λ2$\overrightarrow{OB}$,则λ1-λ2=1.