Question

10．在平行四边形ABCD中，$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\overrightarrow{AC}$，$\frac{\overrightarrow{AB}•\overrightarrow{AD}}{|\overrightarrow{AB}||\overrightarrow{AD}|}$=$\frac{1}{2}$，E为CD的中点，若$\overrightarrow{AC}$•$\overrightarrow{BE}$=3，则|$\overrightarrow{AB}$|=2$\sqrt{3}$．

Answer 1

分析 由$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\overrightarrow{AC}$，可得平行四边形ABCD是菱形．由于$\frac{\overrightarrow{AB}•\overrightarrow{AD}}{|\overrightarrow{AB}||\overrightarrow{AD}|}$=$\frac{1}{2}$，可得$A=\frac{π}{3}$．由于E为CD的中点，$\overrightarrow{AC}$•$\overrightarrow{BE}$=3，利用数量积运算性质、三角形法则即可得出．

解答 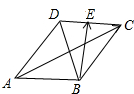解：∵$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\overrightarrow{AC}$，
∴AC平分∠BAD，
因此平行四边形ABCD是菱形．
∵$\frac{\overrightarrow{AB}•\overrightarrow{AD}}{|\overrightarrow{AB}||\overrightarrow{AD}|}$=$\frac{1}{2}$，
∴cosA=$\frac{1}{2}$，A∈（0，π）．
∴$A=\frac{π}{3}$．
∵E为CD的中点，$\overrightarrow{AC}$•$\overrightarrow{BE}$=3，
∴3=$\overrightarrow{AC}$•$\overrightarrow{BE}$=$（\overrightarrow{AB}+\overrightarrow{BC}）$•$（\overrightarrow{BC}-\frac{1}{2}\overrightarrow{AB}）$=$\frac{1}{2}\overrightarrow{AB}•\overrightarrow{BC}$+${\overrightarrow{BC}}^{2}$-$\frac{1}{2}{\overrightarrow{AB}}^{2}$，
设|$\overrightarrow{AB}$|=x，
则3=$\frac{1}{2}{x}^{2}cos\frac{π}{3}$+x²-$\frac{1}{2}{x}^{2}$，
化为x²=12，
解得x=2$\sqrt{3}$．
则|$\overrightarrow{AB}$|=2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．

点评 本题考查了向量数量积运算性质、向量的平行四边形法则、菱形定义、向量三角形法则，考查了推理能力与计算能力，属于中档题．