题目内容
动圆C与定圆C1:(x+3)2+y2=9,C2:(x-3)2+y2=1都外切,求动圆圆心C的轨迹方程.
设所求圆的圆心坐标C(x,y),半径为r,
两定圆的圆心分别是C1,C2,半径分别为3,1.
∵所求圆与两个圆都外切,
∴|CC1|=r+3,|CC2|=r+1,
即|CC1|-|CC2|=2,
根据双曲线定义可知C点的轨迹为以C1,C2为焦点的双曲线的右支,
由2c=6,c=3;2a=2,a=1,∴b=
=2
.
∴C点的轨迹方程为x2-
=1(x≥1).
两定圆的圆心分别是C1,C2,半径分别为3,1.
∵所求圆与两个圆都外切,
∴|CC1|=r+3,|CC2|=r+1,
即|CC1|-|CC2|=2,
根据双曲线定义可知C点的轨迹为以C1,C2为焦点的双曲线的右支,
由2c=6,c=3;2a=2,a=1,∴b=
| 9-1 |
| 2 |
∴C点的轨迹方程为x2-
| y2 |
| 8 |

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
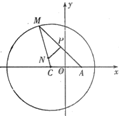
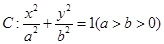 的两个焦点分别为
的两个焦点分别为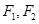 ,且
,且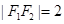 ,点
,点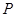 在椭圆上,且
在椭圆上,且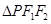 的周长为6.
的周长为6.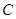 的方程;(2)若点
的方程;(2)若点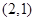 ,不过原点
,不过原点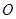 的直线
的直线 与椭圆
与椭圆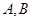 不同两点,设线段
不同两点,设线段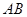 的中点为
的中点为 ,且
,且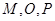 三点共线.设点
三点共线.设点 ,求
,求