题目内容
已知圆O′：（x-1）2+y2=36，点A（-1，0），M是圆上任意一点，线段AM的中垂线l和直线O′M相交于点Q，则点Q的轨迹方程为（ ）
A．
| B．
| C．
| D．
|
如图，联结QA，由于Q在AM的中垂线上，有|QA|=|QM|，
则|QA|+|QO′|=|QM|+|QO′|=|O′M|．
O′M是⊙O′的半径，|O′M|=6．
所以Q到A、O′的距离之和为定值，轨迹为椭圆
椭圆的焦点是A、O′，中心是AO′中点
由于A（-1，0），O′（1，0），
所以c=1，a=3．
则b2=a2-c2=8．
则椭圆的方程是：
+
=1．
即Q的轨迹方程为
+
=1．
故选C．
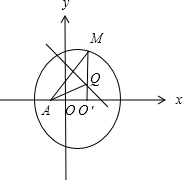
则|QA|+|QO′|=|QM|+|QO′|=|O′M|．
O′M是⊙O′的半径，|O′M|=6．
所以Q到A、O′的距离之和为定值，轨迹为椭圆
椭圆的焦点是A、O′，中心是AO′中点
由于A（-1，0），O′（1，0），
所以c=1，a=3．
则b2=a2-c2=8．
则椭圆的方程是：
| x2 |
| 9 |
| y2 |
| 8 |
即Q的轨迹方程为
| x2 |
| 9 |
| y2 |
| 8 |
故选C．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
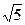+1