题目内容
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),当
为参数),当![]() 时,曲线
时,曲线![]() 上对应的点为
上对应的点为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设曲线![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(I)![]() 的普通方程为
的普通方程为![]() ,
,![]() 的直角坐标方程为
的直角坐标方程为![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)消去参数![]() 即得曲线
即得曲线![]() 的普通方程,根据二倍角公式及
的普通方程,根据二倍角公式及![]() ,消去
,消去![]() 得到曲线
得到曲线![]() 的直角坐标方程;(II)易求曲线
的直角坐标方程;(II)易求曲线![]() 的参数方程为
的参数方程为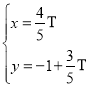 ,代入曲线
,代入曲线![]() 的直角坐标方程得到关于
的直角坐标方程得到关于![]() 的一元二次方程,根据韦达定理即可求得
的一元二次方程,根据韦达定理即可求得![]() 的值.
的值.
试题解析:(I)因为曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
所以曲线![]() 的普通方程为
的普通方程为![]() .
.
又曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]()
(II)当![]() 时,
时,![]() ,
,![]() ,所以点
,所以点![]() .
.
由(I)知曲线![]() 是经过点
是经过点![]() 的直线,设它的倾斜角为
的直线,设它的倾斜角为![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,
所以曲线![]() 的参数方程为
的参数方程为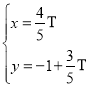 (
(![]() 为参数),
为参数),
将上式代入![]() ,得
,得![]() ,
,
所以![]()

练习册系列答案
相关题目
【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)(i)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中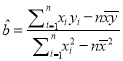 ,
, ![]() .
.