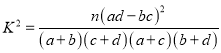Question

【题目】定义：如果函数在定义域内给定区间上存在（），满足，则称函数是上的“平均值函数”， 是它的一个均值点.如是上的平均值函数，0就是他的均值点.

（1）判断函数在区间上是否为平均值函数？若是，求出它的均值点；若不是，请说明理由；

（2）若函数是区间上的平均值函数，试确定实数的取值范围.

Answer 1

【答案】（1）是上的平均值函数，5是它的均值点.（2）

【解析】试题分析：（1）根据“平均值函数”的定义得到关于的方程，判断该方程在内是否有实数根即可；

（2）由题意知方程在内有实数根，求得该方程的根为或（舍去），建立关于的不等式即可。

试题解析：（1）由定义可知，当关于的方程在内有实数根，则函数是上的平均值函数，

由，得，

解得或（舍去），

∴是上的平均值函数，5是它的均值点.

（2）∵是上的平均值函数，

∴关于的方程在内有实数根.

由，

得，

解得或，

又，

∴必为均值点，即.

解得，

故所求实数的取值范围是(.