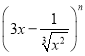题目内容
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
【答案】(I)![]() ; (II)b<-
; (II)b<-![]()
【解析】试题分析:(1)首先对f(x)求导,然后由题设在x=1时有极值10可得f '(1)=0,f(1)=10,解得即可;
(2)x3-x2+bx+1<0在x∈[1,2]恒成立,即b<![]() 在x∈[1,2]恒成立,令g(x)=
在x∈[1,2]恒成立,令g(x)=![]() ,即可求出b的取值范围.
,即可求出b的取值范围.
试题解析:
(I)f '(x)=3x2+2ax+b,由题设有f '(1)=0,f(1)=10
即![]() 解得
解得![]() 或
或![]()
经验证,若![]() 则f '(x)=3x2-6x+3=3(x-1)2
则f '(x)=3x2-6x+3=3(x-1)2
当x>1或x<1时,均有f '(x)>0,可知
此时x=1不是f(x)的极值点,故![]() 舍去
舍去
![]() 符合题意,故
符合题意,故![]() .
.
(II)当a=-1时,f(x)=x3-x2+bx+l
若f(x)<0在x∈[1,2]恒成立,即
x3-x2+bx+1<0在x∈[1,2]恒成立
即b<![]() 在x∈[1,2]恒成立
在x∈[1,2]恒成立
令g(x)=![]() ,则
,则
g '(x)=![]() =
=![]()
(法一:由g '(x)=0解得x=1…)
(法二)由-2x3+x2+1=1-x3+x2(1-x) 可知x∈[1,2]时g '(x)<0
即g(x)=![]() 在x∈[1,2]单调递减
在x∈[1,2]单调递减
(g(x))max=g(2)=-![]()
∴b<-![]() 时,f(x)<0在x∈[1,2]恒成立.
时,f(x)<0在x∈[1,2]恒成立.

练习册系列答案
相关题目