题目内容
11.已知定义在R上的函数f(x)=$\frac{-{2}^{x}+b}{{2}^{x}+a}$是奇函数.(1)求a、b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
分析 (1)根据函数奇偶性的定义和性质建立方程关系即可求a、b的值;
(2)根据函数奇偶性和单调性的性质,将不等式进行转化进行求解即可.
解答 解:(1)∵定义在R上的函数f(x)=$\frac{-{2}^{x}+b}{{2}^{x}+a}$是奇函数.
∴f(0)=0,即$\frac{b-1}{1+a}=0$,得b=1,
则f(x)=$\frac{1-{2}^{x}}{{2}^{x}+a}$,
∵f(x)是奇函数,
∴f(-1)+f(1)=0,
∴$\frac{1-\frac{1}{2}}{\frac{1}{2}+a}$+$\frac{1-2}{2+a}$=0,
解得a=1.
即a=b=1.
(2)∵a=b=1.
∴f(x)=$\frac{1-{2}^{x}}{1+{2}^{x}}$=$\frac{2-(1+{2}^{x})}{1+{2}^{x}}$=-1+$\frac{2}{1+{2}^{x}}$,则f(x)为减函数,
由f(t2-2t)+f(2t2-k)<0
得f(t2-2t)<-f(2t2-k)=f(k-2t2)
即t2-2t>k-2t2恒成立,
即3t2-2t-k>0恒成立,
则判别式△=4+3×4k<0,
解得k<-$\frac{1}{3}$,
即k的取值范围是(-∞,-$\frac{1}{3}$).
点评 本题考查的知识点是函数恒成立问题,函数单调性的性质,函数奇偶性的性质,是函数图象和性质的综合应用,难度中档

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
3.已知命题p:对?x∈R,x2-x-1≥0恒成立.命题q:?x∈R是2x-1≤0成立.则下列命题中为真命题的是( )
| A. | (?p)∧q | B. | (?p)∧(?q) | C. | p∧(?q) | D. | p∧q |
1.f(x)=($\frac{1}{2}$)x-x+1,用二分法求方程($\frac{1}{2}$)x-x+1=0在(0,3)内近似解的过程中,f(1)>0,f(1.5)<0,f(2)<0,f(3)<0,则方程的根落在区间( )
| A. | (1,1.5) | B. | (1.5,2) | C. | (2,3) | D. | 无法确定 |
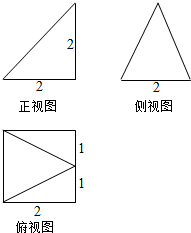 如图是一个几何体的三视图,根据图中所给的数据,求这个几何体的表面积和体积.
如图是一个几何体的三视图,根据图中所给的数据,求这个几何体的表面积和体积.