题目内容
15. 如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
分析 分别求得∠A和∠B,∠C,利用正弦定理求得AC,最后除以时间.
解答  解:根据题意知∠BAC=60°,∠C=45°,∠ABC=105°
解:根据题意知∠BAC=60°,∠C=45°,∠ABC=105°
∴sin∠CBA=sin45°cos60°+cos45°sin60°=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
∴由正弦定理知AC=$\frac{AB}{sinB}$•sinC=$\frac{20}{\frac{\sqrt{2}+\sqrt{6}}{4}}$×$\frac{\sqrt{2}}{2}$=20($\sqrt{3}$-1).
V=$\frac{AC}{30}$=$\frac{2}{3}$($\sqrt{3}$-1)(海里/分钟).
即海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
故答案为:$\frac{2}{3}$($\sqrt{3}$-1).
点评 本题主要考查了正弦定理在解三角形中的应用.考查了学生分析问题和解决实际问题的能力.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 图像上一个动点作函数的切线,则切线倾斜角的范围是_________.
图像上一个动点作函数的切线,则切线倾斜角的范围是_________.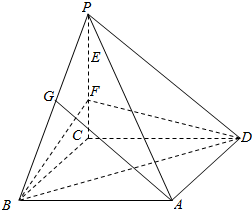 如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?
如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?