Question

【题目】在一次抽样调查中测得样本的5个样本点，数值如下表：

	0.25	0.5	1	2	4
	16	12	5	2	1

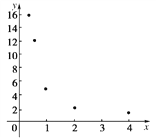
（1）根据散点图判断,哪一个适宜作为关于的回归方程类型？（给出判断即可，不必说明理由）

（2）根据（1）的判断结果试建立与之间的回归方程．（注意或计算结果保留整数）

（3）由（2）中所得设z=+且，试求z的最小值。

参考数据及公式如下：

，，

Answer 1

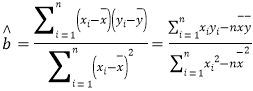
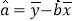
【答案】（1）见解析；（2）6

【解析】分析：（1）由散点图可以判断，适宜作为y关于x的回归方程；

(2)根据散点图可知与近似地呈反比例函数关系，设，令，

则，由散点图可以看出y与t呈近似的线性相关关系．由此可求与之间的回归方程.

（3）由（2）得.由此可求z的最小值.

详解：

（1）由散点图可以判断，适宜作为y关于x的回归方程；

(2)根据散点图可知与近似地呈反比例函数关系，设，令t＝，

则y＝c+kt，原数据变为：

t	4	2	1	0.5	0.25
y	16	12	5	2	1

由散点图可以看出y与t呈近似的线性相关关系．

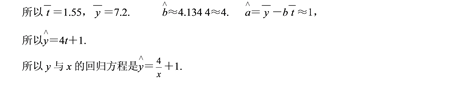
（3）由（2）得.

易知在z是关于x的单调递增函数所以最小值为6..