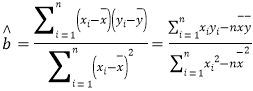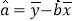题目内容
【题目】设a+b=2，b＞0，当 
+ 
取得最小值时，a= ．
【答案】-2
【解析】解：∵a+b=2，b＞0， ∴ 
+ 
= + 
，（a＜2）；
设f（a）= + ，（a＜2），
作此函数的图象，如右图所示；
利用导数研究其单调性得，
当a＜0时，f（a）=﹣ 
+ 
，
f′（a）= 
﹣ 
= 
，
当a＜﹣2时，f′（a）＜0，当﹣2＜a＜0时，f′（a）＞0，
故函数在（﹣∞，﹣2）上是减函数，在（﹣2，0）上是增函数，
∴当a=﹣2时， + 取得最小值 
；
同理，当0＜a＜2时，得到当a= 时， + 取得最小值 
；．
综合，则当a=﹣2时， + 取得最小值；
故答案为：﹣2．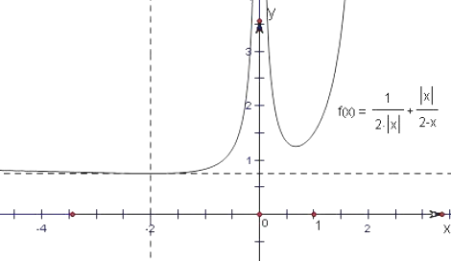
由题意得 + = + ，（a＜2）；从而构造函数f（a）= + ，（a＜2），从而作函数的图象辅助，当a＜0时，f（a）=﹣ + ，f′（a）= ﹣ = ，从而确定函数的单调性及最值；同理确定当0＜a＜2时的单调性及最值，从而解得．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】在一次抽样调查中测得样本的5个样本点，数值如下表：
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
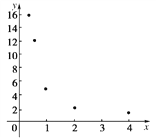
（1）根据散点图判断,
哪一个适宜作为
关于
的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果试建立与之间的回归方程．（注意
或
计算结果保留整数）
（3）由（2）中所得设z=+且
，试求z的最小值。
参考数据及公式如下：
，
，
