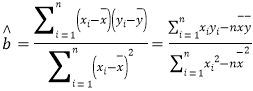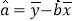题目内容
【题目】已知函数f（x）=2asinωxcosωx+2 
cos2ωx﹣ （a＞0，ω＞0）的最大值为2，且最小正周期为π． （I）求函数f（x）的解析式及其对称轴方程；
（II）若f（α）= 
，求sin（4α+ 
）的值．
【答案】解：（Ⅰ）f（x）=2asinωxcosωx+2 
cos2ωx﹣ =asin2ωx+ cos2ωx= 
sin（2ωx+φ） ∵f（x）的最小正周期为T=π
∴ 
，ω=1，
∵f（x）的最大值为2，
∴ =2，
即a=±1，
∵a＞0，∴a=1．
即f（x）=2sin（2x+ 
）．
由2x+ = 
+kπ，
即x= 
+ 
，（k∈Z）．
（Ⅱ）由f（α）= 
，得2sin（2α+ ）= ，
即sin（2α+ ）= 
，
则sin（4α+ 
）=sin[2（2α+ ） 
]=﹣cos2（2α+ ）=﹣1+2sin2（2α+ ）=﹣1+2×（ ）2=﹣ 
【解析】（Ⅰ）根据条件函数最值和周期，利用三角函数的公式进行化简即可求a和ω的值，即可求出函数的解析式和对称轴方程；（Ⅱ）根据f（a）= 
，利用余弦函数的倍角公式进行化简即可求sin（4α+ 
）的值．
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识，掌握两角和与差的正弦公式：
．
练习册系列答案
相关题目
【题目】在一次抽样调查中测得样本的5个样本点，数值如下表：
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
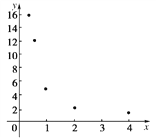
（1）根据散点图判断,
哪一个适宜作为
关于
的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果试建立与之间的回归方程．（注意
或
计算结果保留整数）
（3）由（2）中所得设z=+且
，试求z的最小值。
参考数据及公式如下：
，
，
