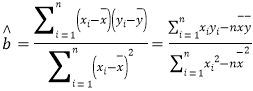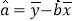题目内容
【题目】已知向量
，设
。
（1）求函数
的最小正周期；
（2）当
时，求函数的最大值及最小值。
【答案】（1）π ；（2）最大值
，最小值-1
【解析】
（1）由两向量的坐标，利用平面向量的数量积运算法则计算得出f（x）解析式，找出ω的值，代入周期公式即可求出最小正周期；
（2）根据x的范围求出这个角的范围，利用正弦函数的定义域与值域就确定出f（x）的最大值与最小值．
（1）∵
（cosx+sinx，sinx），
（cosx﹣sinx，2cosx），
∴f（x）
（cosx+sinx）（cosx﹣sinx）+2sinxcosx＝cos2x﹣sin2x+sin2x＝cos2x+sin2x
sin（2x
），
∵ω＝2，∴T
π；
（2）∵x∈[0，
]，∴2x∈[
，
]，
∴当2x
，即x
时，f（x）min＝﹣1；
当2x
，即x
时，f（x）max，
综上所述，当x时，f（x）min＝﹣1；当x时，f（x）max．
练习册系列答案
相关题目
【题目】在一次抽样调查中测得样本的5个样本点，数值如下表：
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
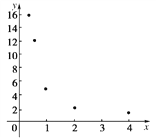
（1）根据散点图判断,
哪一个适宜作为
关于
的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果试建立与之间的回归方程．（注意
或
计算结果保留整数）
（3）由（2）中所得设z=+且
，试求z的最小值。
参考数据及公式如下：
，
，
