题目内容
设直线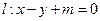 与抛物线
与抛物线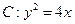 交于不同两点A、B,F为抛物线的焦点。(13分)
交于不同两点A、B,F为抛物线的焦点。(13分)
(1)求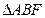 的重心G的轨迹方程;
的重心G的轨迹方程;
(2)如果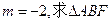 的外接圆的方程。
的外接圆的方程。
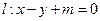 与抛物线
与抛物线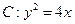 交于不同两点A、B,F为抛物线的焦点。(13分)
交于不同两点A、B,F为抛物线的焦点。(13分)(1)求
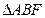 的重心G的轨迹方程;
的重心G的轨迹方程;(2)如果
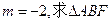 的外接圆的方程。
的外接圆的方程。解:①设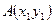 ,
,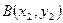 ,
,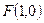 ,重心
,重心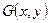 ,
,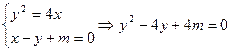
∴△>0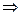
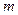 <1且
<1且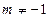 (因为A、B、F不共线)
(因为A、B、F不共线)
故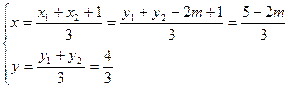
∴重心G的轨迹方程为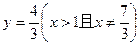 (6分)
(6分)
②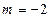 ,则
,则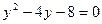 ,设
,设 中点为
中点为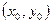
∴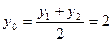 ∴
∴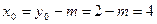
那么AB的中垂线方程为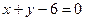
令△ABF外接圆圆心为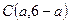
又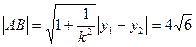 ,C到AB的距离为
,C到AB的距离为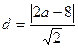
∴
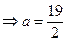 ∴
∴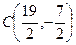 ∴
∴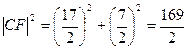
∴所求的圆的方程为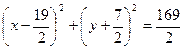 (7分)
(7分)
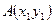 ,
,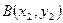 ,
,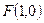 ,重心
,重心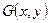 ,
,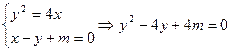
∴△>0
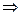
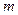 <1且
<1且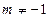 (因为A、B、F不共线)
(因为A、B、F不共线)故
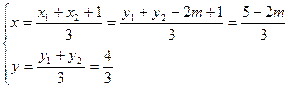
∴重心G的轨迹方程为
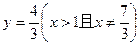 (6分)
(6分)②
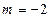 ,则
,则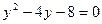 ,设
,设 中点为
中点为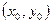
∴
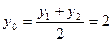 ∴
∴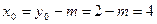
那么AB的中垂线方程为
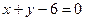
令△ABF外接圆圆心为
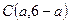
又
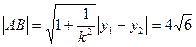 ,C到AB的距离为
,C到AB的距离为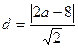
∴

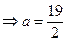 ∴
∴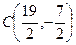 ∴
∴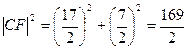
∴所求的圆的方程为
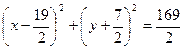 (7分)
(7分)略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
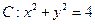 上任取一点
上任取一点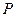 ,过
,过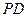 垂直
垂直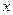 轴于
轴于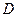 ,且
,且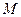 的轨迹
的轨迹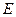 的方程;(2)直线
的方程;(2)直线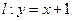 与(1)中曲线
与(1)中曲线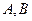 两点,求
两点,求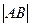 的值.
的值.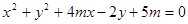 表示圆,则
表示圆,则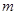 的值为( )
的值为( )


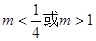
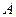 是单位圆与
是单位圆与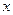 轴正半轴的交点,
轴正半轴的交点,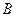 ,
,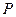 为单位圆上不同的点,
为单位圆上不同的点,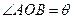 ,
,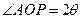 ,
,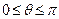 ,
,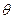 为何值时,
为何值时,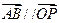 ?
?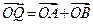 ,则当
,则当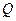 在单位圆上?
在单位圆上?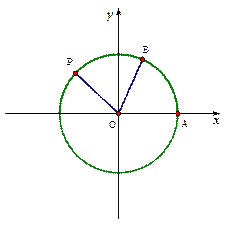
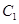 :
: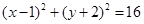 与圆
与圆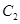 :
: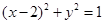 的位置关系是( )
的位置关系是( )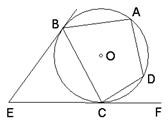
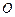 是
是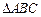 的外接圆,过点
的外接圆,过点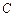 的切线交
的切线交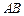 的延长线于点
的延长线于点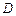 ,
,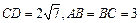 ,则
,则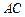 的长为 .
的长为 .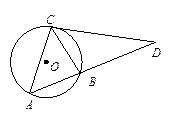
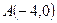 作直线
作直线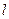 与圆
与圆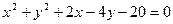 交于
交于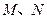 两点,若
两点,若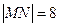 ,则直线
,则直线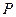 在直线
在直线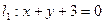 上,过点
上,过点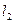 与曲线
与曲线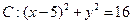 只有一个公共点
只有一个公共点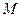 ,则
,则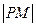 的最小值为__________
的最小值为__________