题目内容
【题目】椭圆C:![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.

(1)求椭圆C的方程;
(2)如果直线l的斜率等于-1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用已知条件求出b,即可求解椭圆方程.
(2)直线l:y=-x+1,设AB坐标,联立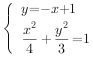 利用韦达定理以及斜率公式求解即可.
利用韦达定理以及斜率公式求解即可.
(3)当直线AB的斜率不存在时,不妨设A,B,求出斜率,即可;当直线AB的斜率存在时,设其为k,求直线AB:y=k(x-1),联立直线与椭圆的方程组,利用韦达定理以及斜率
公式化简求解即可.
解:(1)∵a=2,又c=1,∴![]() ,∴椭圆方程为
,∴椭圆方程为![]()
(2)直线l:y=-x+1,设A(x1,y1)B(x2,y2),
由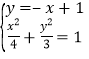 消y得7x2-8x-8=0,有
消y得7x2-8x-8=0,有![]() ,
,![]() .
.
![]()
(3)当直线AB的斜率不存在时,不妨设A(1,![]() ),B(1,-
),B(1,-![]() ),
),
则![]() ,
,![]() ,故k1+k2=2.
,故k1+k2=2.
当直线AB的斜率存在时,设其为k,则直线AB:y=k(x-1),设A(x1,y1)B(x2,y2),
由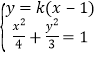 消y得(4k2+3)x2-8k2x+(4k2-12)=0,
消y得(4k2+3)x2-8k2x+(4k2-12)=0,
有![]() ,
,![]() .
.
![]()
=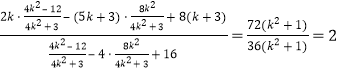

练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: .
.
