题目内容
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,与过右焦点F且斜率为k(k>0)的直线相交于A、B两点.若
,与过右焦点F且斜率为k(k>0)的直线相交于A、B两点.若 =3
=3 ,则k=________.
,则k=________.

 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,与过右焦点F且斜率为k(k>0)的直线相交于A、B两点.若
,与过右焦点F且斜率为k(k>0)的直线相交于A、B两点.若 =3
=3 ,则k=________.
,则k=________.
k=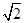
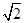
定点F分线段AB成比例,从而分别可以得出A、B两点横坐标之间关系式、纵坐标之间关系式,再把A、B点的坐标代入椭圆方程 =1,四个方程联立方程组,解出根,得出A、B两点的坐标,进而求出直线AB的方程.
=1,四个方程联立方程组,解出根,得出A、B两点的坐标,进而求出直线AB的方程.
由已知e=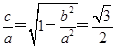 ,所以a=2b,
,所以a=2b,
所以a=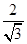 c,b=
c,b=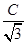 .椭圆方程
.椭圆方程 =1变为
=1变为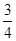 x2+3y2=c2.
x2+3y2=c2.
设A(x1,y1),B(x2,y2),又 =3
=3 ,
,
所以(c-x1,-y1)=3(x2-c,y2),所以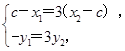 所以
所以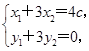
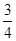
 +3
+3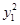 =c2,①
=c2,①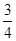
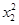 +3
+3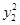 =c2,②
=c2,②
①-9×②,得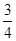 (x1+3x2)(x1-3x2)+3(y1+3y2)(y1-3y2)=-8c2,所以
(x1+3x2)(x1-3x2)+3(y1+3y2)(y1-3y2)=-8c2,所以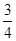 ×4c(x1-3x2)=-8c2,
×4c(x1-3x2)=-8c2,
所以x1-3x2=-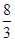 c,所以x1=
c,所以x1=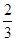 c,x2=
c,x2=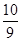 c.从而y1=-
c.从而y1=-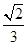 c,y2=
c,y2=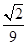 c,
c,
所以A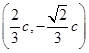 ,B
,B ,故k=
,故k=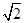 .
.
 =1,四个方程联立方程组,解出根,得出A、B两点的坐标,进而求出直线AB的方程.
=1,四个方程联立方程组,解出根,得出A、B两点的坐标,进而求出直线AB的方程.由已知e=
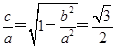 ,所以a=2b,
,所以a=2b,所以a=
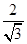 c,b=
c,b=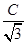 .椭圆方程
.椭圆方程 =1变为
=1变为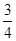 x2+3y2=c2.
x2+3y2=c2.设A(x1,y1),B(x2,y2),又
 =3
=3 ,
,所以(c-x1,-y1)=3(x2-c,y2),所以
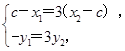 所以
所以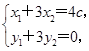
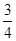
 +3
+3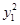 =c2,①
=c2,①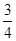
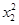 +3
+3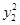 =c2,②
=c2,②①-9×②,得
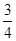 (x1+3x2)(x1-3x2)+3(y1+3y2)(y1-3y2)=-8c2,所以
(x1+3x2)(x1-3x2)+3(y1+3y2)(y1-3y2)=-8c2,所以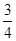 ×4c(x1-3x2)=-8c2,
×4c(x1-3x2)=-8c2,所以x1-3x2=-
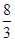 c,所以x1=
c,所以x1=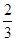 c,x2=
c,x2=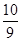 c.从而y1=-
c.从而y1=-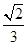 c,y2=
c,y2=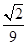 c,
c,所以A
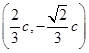 ,B
,B ,故k=
,故k=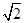 .
.
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
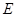 的方程为
的方程为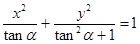 ,其中
,其中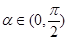 .
.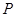 ,证明:点
,证明:点 (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为
 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足 (
( 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数 的取值范围?
的取值范围?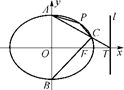
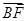 =3
=3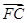 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为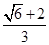 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标. +y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
 =m
=m +n
+n ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程; 的焦距为2,且过点
的焦距为2,且过点 .
. ,
, ,过点
,过点 与椭圆C交于
与椭圆C交于 两点.
两点. 时,求
时,求 的长;
的长; 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当 的离心率为
的离心率为 ,短轴长是2.
,短轴长是2.
 时,求k的取值范围.
时,求k的取值范围. =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合. ,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点.
,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点. ,求椭圆的方程;
,求椭圆的方程; ·
· <7时,求椭圆离心率的取值范围.
<7时,求椭圆离心率的取值范围.